▷ Derivada da secante (fórmula e exercícios resolvidos)

Aqui você descobrirá como derivar a secante de uma função. Além disso, você poderá ver diversos exercícios resolvidos passo a passo sobre a derivada da secante. E por fim, você encontrará a demonstração da fórmula desse tipo de derivada trigonométrica.

Qual é a derivada da secante?

A derivada da secante de x é igual ao produto da secante de x pela tangente de x.

$f(x)=\text{sec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x)\cdot \text{tan}(x)$

Ao aplicar fórmulas trigonométricas, a derivada da secante de x também pode ser definida como o quociente do seno de x dividido pelo quadrado do cosseno de x.

$f'(x)=\text{sec}(x)\cdot \text{tan}(x)=\cfrac{1}{\text{cos}(x)}\cdot \cfrac{\text{sen}(x)}{\text{cos}(x)}=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

E se aplicarmos a regra da cadeia, a derivada da secante de uma função é o produto da secante da função vezes a tangente da função vezes a derivada da função.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

Em resumo, a fórmula para a derivada da função secante é a seguinte:

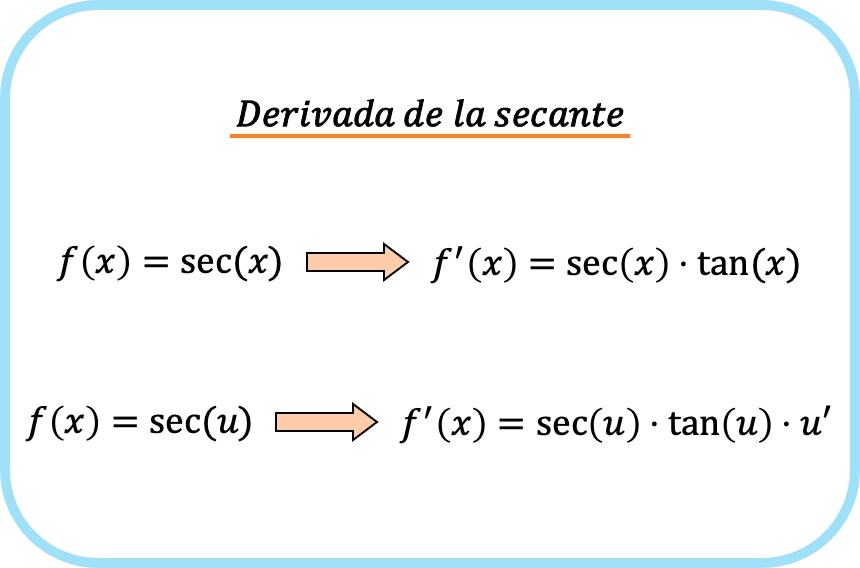
Exemplos de derivada da secante

Depois de vermos qual é a fórmula da derivada da secante, resolveremos vários exemplos deste tipo de derivadas trigonométricas.

Exemplo 1: Derivada da secante de 2x

Neste exemplo veremos quanto vale a derivada da secante de 2x:

$f(x)=\text{sec}(2x)$

Para derivar a secante da função 2x, você deve usar sua fórmula correspondente. Além disso, no argumento secante temos uma função diferente de x, portanto precisamos aplicar a regra da cadeia.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

A função 2x é linear, então sua derivada é 2. Portanto, para encontrar a derivada, simplesmente substituímos u por 2x e u’ por 2 na fórmula:

$f(x)=\text{sec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(2x)\cdot \text{tan}(2x)\cdot 2$

Exemplo 2: Derivada da secante de x ao quadrado

Neste exercício veremos qual é a derivada da secante de x ao quadrado:

$f(x)=\text{sec}(x^2)$

Para derivar a secante de uma função você pode usar uma das duas fórmulas vistas acima, mas neste caso iremos diferenciar a função com a fórmula de multiplicação entre a secante e a tangente.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

A derivada de x elevada à potência de 2 dá 2x, então a derivada da secante de x ao quadrado é:

$f(x)=\text{sec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x^2)\cdot \text{tan}(x^2)\cdot 2x$

Exemplo 3: Derivada do cubo secante de um polinômio

$f(x)=\text{sec}^3(x^5+4x^2-3)$

A regra para a derivada da secante de uma função é:

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

Mas neste caso devemos derivar uma função composta, pois a secante é elevada à terceira potência e, além disso, em seu argumento temos uma função polinomial. Então, para derivar toda a função, precisamos aplicar a regra da cadeia:

$\begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}$

Exercícios resolvidos sobre a derivada de uma secante

Derive as seguintes funções secantes:

$\text{A) }f(x)=\text{sec}(x^6-6x^3)$

$\text{B) }f(x)=\text{sec}^4(5x^4)$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)$

Veja a solução

$\text{A) }f(x)=\text{sec}(x^6-6x^3)\cdot \text{tan}(x^6-6x^3)\cdot (6x^5-18x^2)$

$\begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)\cdot \text{tan}\bigl(\ln(x)\bigr)\cdot \cfrac{1}{x}$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)\cdot \text{tan}\left(e^{x^2+3x}\right)\cdot e^{x^2+3x}\cdot (2x+3)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)\cdot \text{tan}\left(\sqrt{5x+1}\right)\cdot \cfrac{5}{2\sqrt{5x+1}}$

Demonstração da fórmula da derivada da secante

A seguir, provaremos a fórmula da derivada da secante. Embora obviamente não seja necessário saber de cor a prova, é sempre bom entender de onde vêm as fórmulas.

Matematicamente, a definição da secante é o inverso multiplicativo do cosseno:

$f(x)=\text{sec}(x)=\cfrac{1}{\text{cos}(x)}$

Portanto, podemos tentar derivar a secante usando a regra do quociente:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

E, como vimos na primeira seção, a expressão anterior pode ser convertida na fórmula da derivada da secante. Para fazer isso, separamos a fração em duas frações diferentes:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\cdot \cfrac{1}{\text{cos}(x)}$

A divisão do seno pelo cosseno equivale à tangente, substituímos portanto o referido quociente pela tangente:

$f'(x)=\text{tan}(x)\cdot \cfrac{1}{\text{cos}(x)}$

De acordo com a definição matemática da função secante, o cosseno é o seu multiplicativo inverso. Então, substituindo um dividido pelo cosseno pela secante, chegamos à fórmula da sua derivada:

$f'(x)=\text{tan}(x)\cdot \text{sec}(x)$

Qual é a derivada da secante?

Exemplos de derivada da secante

Exemplo 1: Derivada da secante de 2x

Exemplo 2: Derivada da secante de x ao quadrado

Exemplo 3: Derivada do cubo secante de um polinômio

Exercícios resolvidos sobre a derivada de uma secante

Demonstração da fórmula da derivada da secante

Deixe um comentário Cancelar resposta