▷ Derivada da cotangente (fórmula e exemplos)

Neste artigo, veremos como derivar a cotangente de uma função. Você encontrará exemplos de derivadas da cotangente e até exercícios resolvidos passo a passo. Finalmente, provamos a fórmula da derivada da cotangente.

Fórmula para a derivada da cotangente

A derivada da cotangente de x é igual a menos um sobre o quadrado do seno de x. A derivada da cotangente de x também é igual a menos o quadrado da cossecante de x e menos a soma de um mais o quadrado da cotangente de x.

$\begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}$

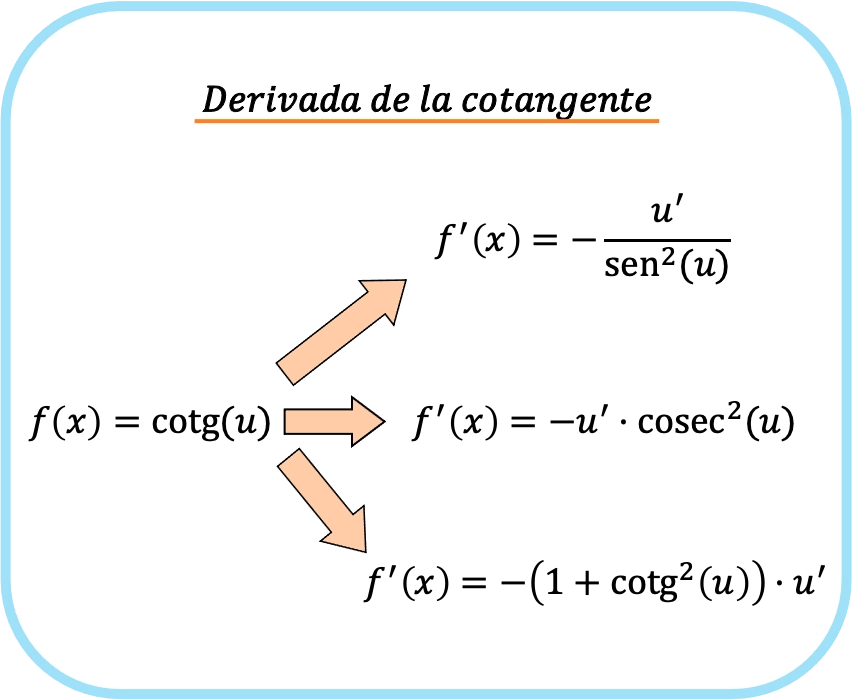
Se a cotangente do argumento for uma função diferente de x, as fórmulas da derivada da cotangente de uma função são as mesmas das anteriores, mas multiplicando as expressões pela derivada da função do argumento.

$\begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}$

Isto significa que existem três fórmulas diferentes para encontrar a derivada da cotangente. Mas, logicamente, não é necessário usar todas as três fórmulas, mas você pode derivá-las com a fórmula que preferir.

Exemplos de derivada da cotangente

Agora que vimos a fórmula da derivada da cotangente de uma função, nesta seção resolveremos vários exemplos deste tipo de derivadas trigonométricas.

Exemplo 1: Derivada da cotangente de 2x

Neste exemplo veremos qual é a derivada da cotangente da função 2x.

$f(x)=\text{cotg}(2x)$

Como vimos, para calcular a derivada da cotangente você pode usar uma das três fórmulas vistas acima. Neste caso usaremos a fórmula senoidal:

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

Como 2x é um termo de primeiro grau, sua derivada é 2. Portanto, a derivada da cotangente de 2x é menos dois dividido pelo quadrado do seno de 2x:

$f(x)=\text{cotg}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\text{sen}^2(2x)}$

Exemplo 2: Derivada da cotangente de x ao quadrado

No segundo exemplo determinaremos qual é a derivada da cotangente de x ao quadrado.

$f(x)=\text{cotg}(x^2)$

Neste exemplo, a função do argumento cotangente não é x, portanto devemos aplicar a regra da cadeia para diferenciar a cotangente.

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

A derivada de x ao quadrado é 2x, então a derivada da cotangente de x ² é:

$f(x)=\text{cotg}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\text{sen}^2(x^2)}$

Exemplo 3: Derivada da cotangente ao cubo

Finalmente, descobriremos quanto é a derivada da cotangente ao cubo de uma função polinomial:

$f(x)=\text{cotg}^3(x^5-6x^2+10)$

Neste caso temos uma composição de funções, então precisamos usar a regra da cadeia com a fórmula da derivada de uma potência para encontrar a derivada da cotangente:

$\displaystyle f'(x)=-3\cdot\text{cotg}^2(x^5-6x^2+10)\cdot\frac{5x^4-12x}{\text{sen}^2(x^5-6x^2+10)}$

Exercícios resolvidos sobre a derivada da cotangente

Calcule a derivada das seguintes funções cotangentes:

$\text{A) } f(x)=\text{cotg}(5x)$

$\text{B) } f(x)=\text{cotg}(2x^4+10x-3)$

$\text{C) } \displaystyle f(x)=\text{cotg}^5\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{cotg}\left(e^{x^2}\right)$

$\text{E) } f(x)=\text{cotg}\bigl(\ln(x^2)\bigr)$

$\text{F) } f(x)=\text{cotg}\left(\sqrt{8x}\right)$

Veja a solução

$\text{A) } f'(x)=-\cfrac{5}{\text{sen}^2(5x)}$

$\text{B) } f'(x)=-\cfrac{8x+10}{\text{sen}^2(2x^4+10x-3)}$

$\text{C) } \displaystyle f'(x)=5\cdot \text{cotg}^4\left(\frac{x}{2}\right)\cdot \left(-\frac{1}{\text{sen}^2\left(\frac{x}{2}\right)}\right)\cdot \frac{1}{2}=-\frac{5\cdot \text{cotg}^4\left(\frac{x}{2}\right)}{2\cdot \text{sen}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=-\cfrac{2x\cdot e^{x^2}}{\text{sen}^2(e^{x^2})}$

$\text{E) } f'(x)=-\cfrac{\cfrac{2x}{x^2}}{\text{sen}^2\bigl(\ln(x^2)\bigr)}=-\cfrac{2}{x\cdot\text{sen}^2\bigl(\ln(x^2)\bigr)}$

$\text{F) } f'(x)=-\cfrac{\frac{8}{2\sqrt{8x}}}{\text{sen}^2\left(\sqrt{8x}\right)}=-\cfrac{4}{\sqrt{8x}\cdot \text{sen}^2\left(\sqrt{8x}\right)}$

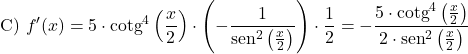
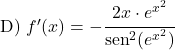
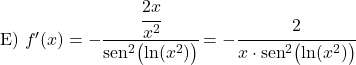
Prova da derivada da cotangente

Nesta seção final, demonstraremos a fórmula da derivada da cotangente. Para isso, partiremos da definição matemática da função cotangente, que é igual ao cosseno dividido pelo seno:

$\text{cotg}(x)=\cfrac{\text{cos}(x)}{\text{sen}(x)}$

Agora diferenciamos a função aplicando a regra da derivada de um quociente;

$\displaystyle\bigl(\text{cotg}(x)\bigr)'=\left(\frac{\text{cos}(x)}{\text{sen}(x)}\right)'$

$\text{cotg}'(x)=\cfrac{-\text{sen}(x)\cdot \text{sen}(x)-\text{cos}(x)\cdot \text{cos}(x) }{\text{sen}^2(x)}$

$\text{cotg}'(x)=\cfrac{-\text{sen}^2(x)-\text{cos}^2(x)}{\text{sen}^2(x)}$

Pegamos o fator comum no denominador e removemos o sinal negativo da fração:

$\text{cotg}'(x)=\cfrac{-\bigl(\text{sen}^2(x)+\text{cos}^2(x)\bigr)}{\text{sen}^2(x)}$

$\text{cotg}'(x)=-\cfrac{\text{sen}^2(x)+\text{cos}^2(x)}{\text{sen}^2(x)}$

Por outro lado, sabemos que o quadrado do seno mais o quadrado do cosseno é igual a um graças à identidade trigonométrica fundamental.

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{cotg}'(x)=-\cfrac{1}{\text{sen}^2(x)}$

E assim obtivemos a primeira fórmula para a derivada da cotangente. Da mesma forma, a cossecante é o inverso multiplicativo do seno, então a segunda regra da derivada da cotangente também está provada:

$\text{cotg}'(x)=-\text{sec}^2(x)$

Por fim, a terceira fórmula da derivada desta função trigonométrica pode ser comprovada transformando a fração da etapa anterior em uma soma de frações: