Neste artigo explicamos como derivar a cossecante hiperbólica de uma função. Além disso, você poderá ver vários exemplos resolvidos da derivada da cossecante hiperbólica.
Fórmula para a derivada da cossecante hiperbólica
A derivada da cossecante hiperbólica de x é igual a menos a cossecante hiperbólica de x vezes a cotangente hiperbólica de x.
![]()
Portanto, a derivada da cossecante hiperbólica de uma função é menos o produto da cossecante hiperbólica da função vezes a cotangente hiperbólica da função vezes a derivada da referida função.
![]()
Resumindo, a fórmula para derivar a cossecante de uma função é:
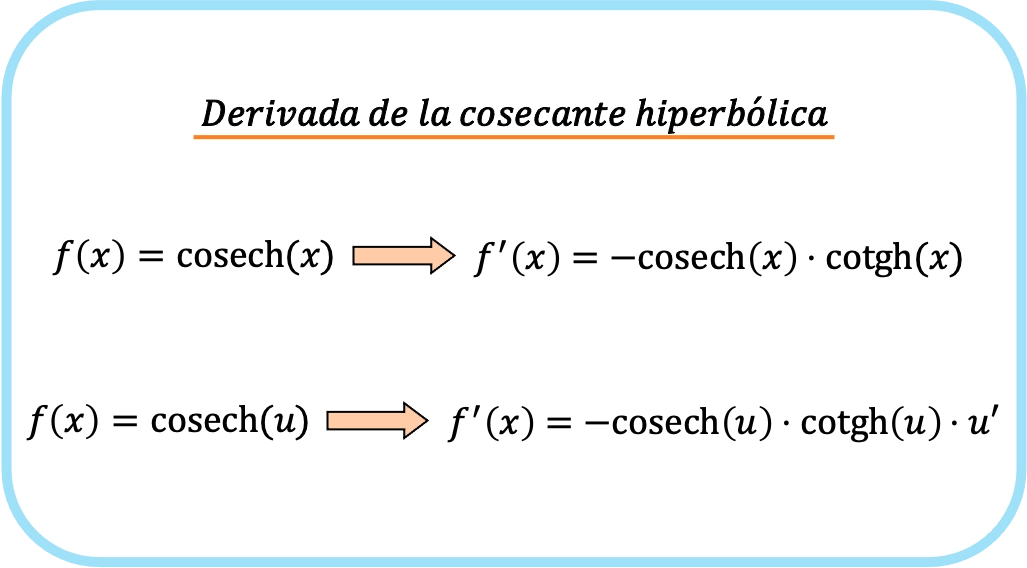
Na verdade, as duas expressões anteriores correspondem a uma única fórmula, a diferença é que a regra da cadeia é aplicada na segunda fórmula.
Exemplos de derivada da cossecante hiperbólica
Depois de ver qual é a fórmula da derivada da cossecante hiperbólica, aqui estão vários exemplos trabalhados desse tipo de derivada trigonométrica.
Exemplo 1
Neste primeiro exemplo, derivaremos a cossecante hiperbólica de x ao quadrado:
![]()
A função do argumento da cossecante hiperbólica é diferente de x, então precisamos usar a fórmula da derivada da cossecante hiperbólica com a regra da cadeia.
![]()
Então, para derivar essa função trigonométrica, basta substituir os valores da fórmula anterior, ou seja, no argumento da cossecante hiperbólica e da tangente hiperbólica, colocamos x 2 , e multiplicamos tudo pela derivada de x ao quadrado, que é 2x:
![]()
Exemplo 2
Neste exercício, veremos quanto é a derivada da cossecante hiperbólica de x ao cubo:
![]()
Para encontrar a derivada da cossecante hiperbólica de uma função, aplicamos sua fórmula:
![]()
A derivada de x ao cubo é 3x 2 , então a derivada de toda a função é:
![]()