Aqui você descobrirá como derivar a função cosseno (fórmula). Você poderá ver exemplos de derivadas de funções cosseno e praticar exercícios passo a passo. Além disso, mostramos a prova da fórmula, qual é a segunda derivada do cosseno e até mesmo a derivada do cosseno inverso.
Qual é a derivada do cosseno?
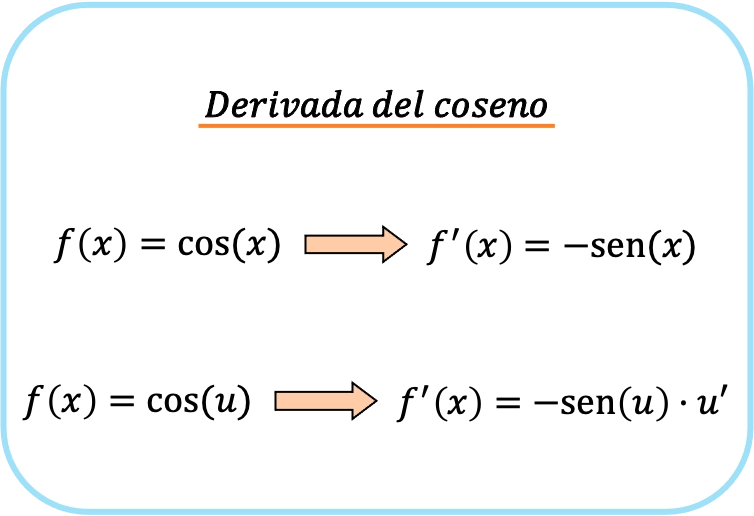
A derivada da função cosseno é a função seno com sinal modificado. Em outras palavras, a derivada do cosseno de x é igual a menos o seno de x.
![]()
Se houver uma função no argumento do cosseno, a derivada do cosseno é o produto de menos o seno dessa função vezes a derivada da função.
![]()
A segunda fórmula é equivalente à primeira fórmula, mas aplicando a regra da cadeia. Então, em resumo, a fórmula da derivada do cosseno é a seguinte:
Exemplos de derivadas de cosseno
Agora que sabemos o que é a fórmula do cosseno, explicaremos vários exemplos desse tipo de derivadas trigonométricas para que você não tenha dúvidas sobre como derivar a função cosseno.
Exemplo 1: Derivada do cosseno de 2x
![]()
No argumento do cosseno não temos um único x, mas sim uma função mais complexa. Portanto, precisamos usar a seguinte fórmula para derivar o cosseno:
![]()
Como a derivada de 2x é 2, a derivada do cosseno de 2x será menos o seno de 2x multiplicado por 2.
![]()
Exemplo 2: Derivada do cosseno de x ao quadrado
![]()
Como no exemplo anterior, no argumento do cosseno temos uma função diferente de x, então usaremos a regra da cadeia para derivar o cosseno:
![]()
Então, a derivada de x 2 é 2x, portanto, a derivada do cosseno de x elevado à potência de 2 é:
![]()
Exemplo 3: Derivada do cosseno ao cubo
![]()
A função cosseno neste exemplo é composta por outra função, portanto precisamos aplicar a seguinte fórmula para resolver a derivada:
![]()
Assim, aplicando a fórmula, chegamos à derivada da função:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73284bcfb1d5647b2304e323e7fbaedf_l3.png)
➤ Para derivar esta função, você também deve usar a fórmula da derivada de uma função potencial .
Segunda derivada do cosseno
A seguir veremos que a segunda derivada do seno pode ser facilmente calculada, graças às características das funções trigonométricas.
➤ Nota: Para entender o seguinte, você precisa saber qual é a derivada do seno .
A segunda derivada do cosseno de x é menos o cosseno de x. Isto pode parecer estranho, mas matematicamente é assim. Na verdade, a derivada do seno é o cosseno e, portanto, diferenciando duas vezes o cosseno de x, o cosseno é novamente obtido, mas com um sinal modificado.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0d9dda8a4031c367120b1f950da4391_l3.png)
Esta propriedade muda se o argumento do cosseno não for x, pois neste caso arrastamos o termo da regra da cadeia:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d86bd6508f06b0723153b3b9254c1f_l3.png)
Derivada do cosseno inverso
Todas as funções trigonométricas têm uma função inversa e, como tal, a função cosseno também pode ser invertida. Da mesma forma, o cosseno inverso é diferenciável.
A derivada do cosseno inverso de uma função é menos a derivada da função dividida pela raiz quadrada de um menos o quadrado da referida função.
![]()
Lembre-se de que o cosseno inverso também é chamado de arco cosseno.
Por exemplo, a derivada do cosseno inverso de 3x é:
![]()
Exercícios resolvidos sobre a derivada do cosseno
Calcule a derivada das seguintes funções cosseno:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f4645fb77435daec6f696cffbd54884_l3.png)
Prova da derivada do cosseno
Por fim, demonstraremos matematicamente a fórmula da derivada do cosseno de x. Para isso, utilizaremos a definição da derivada, que corresponde ao seguinte limite:
![]()
Vamos provar o cosseno, então a função é cos(x):
![]()
Não podemos resolver este limite por substituição, porque terminaríamos na indeterminação. No entanto, podemos expressar o cosseno de uma soma de outra forma, aplicando a seguinte identidade trigonométrica:
![]()
![]()
O próximo passo é separar a fração em duas frações e pegar o fator comum do cosseno:
![Rendered by QuickLaTeX.com \displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7c1cd89cf290b01d7d72fc8084f6529_l3.png)
O limite de uma subtração é igual à subtração dos limites, portanto:
![]()
O cosseno de x e o seno de x não dependem de h, então podemos extraí-los fora dos limites:
![]()
Utilizando o cálculo dos limites por equivalentes infinitesimais, concluímos que o primeiro limite é 0 e o segundo limite é 1. Portanto:
![]()
![]()
E já chegamos à fórmula da derivada da função cosseno, então a igualdade está provada.