Linhas perpendiculares (perpendicularidade) -

Nesta página você encontrará tudo sobre retas perpendiculares: o que são, quando duas retas são perpendiculares, como calcular uma reta perpendicular a outra, suas propriedades,… Além disso, você poderá ver exemplos e poderá pratique com exercícios resolvidos passo a passo.

O que são duas linhas perpendiculares?

Em matemática, duas retas são perpendiculares quando se cruzam em um ponto formando quatro ângulos retos iguais (90º).

Além disso, os vetores de direção de duas retas perpendiculares também devem ser perpendiculares.

A perpendicularidade de duas linhas é geralmente indicada pelo símbolo

$\perp .$

Por outro lado, lembre-se que no plano existem 4 possibilidades no conceito de posição relativa entre duas retas: duas retas podem ser secantes, perpendiculares, coincidentes ou paralelas. Se desejar, você pode verificar o significado de cada tipo de linha em nosso site.

Como você sabe se duas linhas são perpendiculares?

Existem duas maneiras de determinar quando duas retas são perpendiculares, a partir de seus vetores de direção ou por suas inclinações . Abaixo você encontra a explicação de ambos os métodos, embora tenham a mesma finalidade, recomendamos que você saiba fazer os dois procedimentos, pois cada um depende de como as linhas são expressas.

Dos vetores de direção das linhas

Uma maneira de saber quando duas retas são perpendiculares é usar os vetores de direção das retas em questão. Lembre-se que o vetor direção é aquele vetor que indica a direção de uma reta.

Os vetores de direção de duas retas perpendiculares também são mutuamente ortogonais. Portanto, se o produto escalar dos vetores de direção de duas retas for igual a 0, significa que as retas são perpendiculares.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Vamos ver como a perpendicularidade de duas retas é determinada usando um exemplo:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Ambas as linhas são expressas como equações paramétricas, portanto os componentes do vetor de direção de cada linha são os números na frente do parâmetro

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Uma vez conhecido o vetor diretor de cada reta, verificamos se elas são perpendiculares calculando o produto entre os vetores:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

O produto escalar dos dois vetores é zero, então as retas são perpendiculares.

Inclinações de linha

Outra maneira de determinar se duas retas são perpendiculares é usar suas inclinações. Lembre-se de que a inclinação de uma reta é o coeficiente

$m$

da equação explícita e da equação ponto-inclinação de uma reta.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

E a inclinação de uma reta também pode ser obtida a partir dos coeficientes

$A$

$B$

da equação implícita (ou geral) de uma reta:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Assim, as inclinações de duas retas perpendiculares são inversas e de sinais opostos, ou seja, a seguinte igualdade é sempre satisfeita:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Portanto , se o produto das inclinações de duas retas diferentes for igual a -1, isso implica que as retas são perpendiculares:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Por exemplo, as duas linhas a seguir são perpendiculares:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

Podemos mostrar que são duas retas perpendiculares entre si a partir dos seus coeficientes angulares. A inclinação de cada linha é:

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Agora multiplicamos as inclinações:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

O produto entre as duas inclinações é equivalente a -1, o que na verdade significa duas linhas perpendiculares entre si.

Como calcular uma linha perpendicular a outra?

Embora possa parecer difícil de fazer, encontrar uma reta perpendicular a outra é bastante simples, para isso basta um vetor de direção perpendicular à reta e um ponto que pertença à reta.

A única dificuldade é que, como antes, o procedimento depende do tipo de equação em que as retas são expressas. Porque uma linha perpendicular a outra pode ser calculada a partir dos vetores de direção ou das inclinações .

Do vetor de direção da direita

Uma linha perpendicular a outra linha dada pode ser encontrada usando seu vetor de direção. Vamos ver como isso é feito com um exemplo:

Calcule a linha perpendicular à linha
$r$

o que passa pelo ponto

$P(5,-1)$

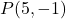
. ser direto

$r:$

$\displaystyle r : \ 3x+2y-1=0$

A primeira coisa que precisamos fazer é identificar o vetor diretor da reta. Neste caso, a reta é definida na forma de uma equação geral (ou implícita), portanto, as coordenadas cartesianas do vetor diretor da reta podem ser obtidas com os coeficientes A e B da reta:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

E uma vez que conhecemos o vetor diretor da reta, devemos calcular um vetor perpendicular a ela. Para isso, basta inserir as coordenadas do vetor e alterar o sinal de uma delas (a que você deseja):

$\vv{\text{v}}_\perp =(3,2)$

Então agora sabemos o vetor diretor da reta. A equação implícita da reta será, portanto, a seguinte:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Portanto, basta determinar o parâmetro C. Para isso, substituímos o ponto que pertence à reta em sua equação e resolvemos a equação resultante:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

Concluindo, a equação da reta perpendicular é:

$\bm{2x-3y-13=0}$

Da inclinação da linha

Outra maneira de encontrar uma reta perpendicular a uma determinada reta é a partir de sua inclinação. Vejamos como esse tipo de problema é resolvido através de um exemplo:

Calcule a linha perpendicular à linha
$r$

o que passa pelo ponto

$P(0,1)$

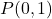
. ser direto

$r:$

$\displaystyle r : \ y=4x-3$

A inclinação da linha

$r$

Leste:

$m_r = 4$

Depois de sabermos a inclinação da reta, precisamos encontrar a inclinação da reta perpendicular. Como vimos nas seções acima, as inclinações de duas retas perpendiculares são inversas e têm seu sinal alterado. Portanto, para determinar a inclinação da reta perpendicular, precisamos inverter a inclinação encontrada e alterar seu sinal:

$m_\perp =-\cfrac{1}{4}$

A equação explícita da reta perpendicular será, portanto, a seguinte:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Finalmente, calculamos a ordenada na origem da reta perpendicular substituindo as coordenadas do ponto na equação da reta:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

Resumindo, a equação da reta perpendicular é:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Propriedades de linhas perpendiculares

Todas as linhas perpendiculares têm as seguintes características:

Relação simétrica : se uma linha é perpendicular a outra linha, essa linha também é perpendicular à primeira linha.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Propriedade não reflexiva : Obviamente, nenhuma linha pode ser perpendicular a si mesma.

$r \ \cancel{\bm{\perp}}} \ r$

Teorema: Na geometria euclidiana (em R2), qualquer par de retas perpendiculares a uma terceira reta deve ser necessariamente paralelo. Ou seja, se uma reta é perpendicular a outra reta e essa reta também é perpendicular a uma terceira reta, a primeira e a última reta são paralelas.

Problemas resolvidos de linhas perpendiculares

Exercício 1

Quais das seguintes retas são perpendiculares à reta

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

veja solução

A inclinação da linha

$r$

é 3:

$m_r=3$

E as inclinações de duas retas perpendiculares são inversas e de sinais opostos, portanto a inclinação de qualquer reta perpendicular à reta

$r$

devemos ser:

$m_\perp=-\cfrac{1}{3}$

Para que as linhas perpendiculares à linha

$r$

são aqueles cuja inclinação é igual a

$-\cfrac{1}{3}$

. Ou seja, as linhas

$\bm{b}$

$\bm{e}.$

Exercício 2

Determine se as duas retas a seguir são perpendiculares:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

veja solução

o certo

$r$

é expresso na forma de uma equação paramétrica, tal que os componentes do vetor de direção da referida reta são os números na frente do parâmetro

$t:$

$\vv{\text{v}}_r =(-1,-3)$

Por outro lado, a linha reta

$s$

é definido na forma de uma equação contínua, então as coordenadas de seu vetor de direção são os números dos denominadores:

$\vv{\text{v}}_s =(4,6)$

Uma vez conhecido o vetor diretor de cada reta, podemos verificar se elas são perpendiculares calculando o produto dos dois vetores:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

O produto escalar dos dois vetores é diferente de zero, então as linhas não são perpendiculares .

Exercício 3

Encontre a linha perpendicular à linha

$r$

o que passa pelo ponto

$P(-2,1)$

. ser direto

$r:$

$\displaystyle r : \ 4x-y+5=0$

veja solução

A primeira coisa que precisamos fazer é identificar o vetor diretor da reta. Neste caso, a reta é definida na forma de uma equação geral (ou implícita), portanto seu vetor direção é:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Depois de conhecermos o vetor diretor da reta, precisamos calcular um vetor perpendicular a ela. Para isso, basta inserir as coordenadas do vetor e alterar o sinal de uma delas (a que você deseja):

$\vv{\text{v}}_\perp =(4,-1)$

A equação implícita da reta será, portanto, a seguinte:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

Portanto, é suficiente determinar a incógnita C. Para fazer isso, substituímos o ponto pelo qual a reta passa em sua equação:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Finalmente, a equação da reta perpendicular é:

$\bm{-x-4y+2=0}$

Exercício 4

Encontre a equação ponto-inclinação da linha perpendicular à linha

$r$

o que passa pelo ponto

$P(3,-2)$

. ser direto

$r:$

$\displaystyle r : \ y=5x+1$

veja solução

A inclinação da linha

$r$

Leste:

$m_r = 5$

Depois de sabermos a inclinação da reta, precisamos encontrar a inclinação da reta perpendicular. Para isso, basta inverter a inclinação encontrada e alterar o seu sinal:

$m_\perp =-\cfrac{1}{5}$

Finalmente, basta substituir a inclinação encontrada e as coordenadas do ponto na equação ponto-inclinação da reta:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Exercício 5

o certo

$r$

passa pelos pontos (2,1) e (4,2), e a reta

$s$

passa pelos pontos (-1,2) e (1,-2). Determine se essas são duas linhas perpendiculares ou não.

veja solução

Para verificar se se trata de duas retas perpendiculares, calcularemos suas inclinações e depois veremos se respeitam a relação perpendicular. Lembre-se de que a fórmula para a inclinação de uma reta é:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

A inclinação da linha

$r$

Leste:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

A inclinação da linha

$s$

Leste:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

Para verificar a perpendicularidade das duas retas, devemos ver se a inclinação de uma reta é o inverso da outra. Neste caso, as duas inclinações são inversas e também possuem sinais opostos, portanto as duas retas são perpendiculares entre si.

Exercício 6

Calcule o valor de

$k$

de modo que as duas linhas a seguir sejam perpendiculares:

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

veja solução

As duas retas são expressas na forma de uma equação implícita (ou geral), e o vetor de direção de uma equação implícita da reta é:

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Portanto, o vetor direção de cada linha seria:

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

Para que duas retas sejam perpendiculares, o produto escalar de seus vetores de direção deve ser zero. Portanto, aplicaremos esta condição para encontrar o valor da incógnita

$k:$