▷ Como fazer a decomposição polinomial de um número ✅

Nesta página explicamos como fazer a decomposição polinomial (ou expressão) de um número. Aqui você pode ver exemplos de decomposições polinomiais e, além disso, encontrará passo a passo exercícios resolvidos para praticar.

O que é decomposição polinomial de um número?

Em matemática, a decomposição polinomial de um número consiste em expressar esse número em uma soma, de modo que cada termo da soma seja um produto de cada dígito do número por uma potência de base 10.

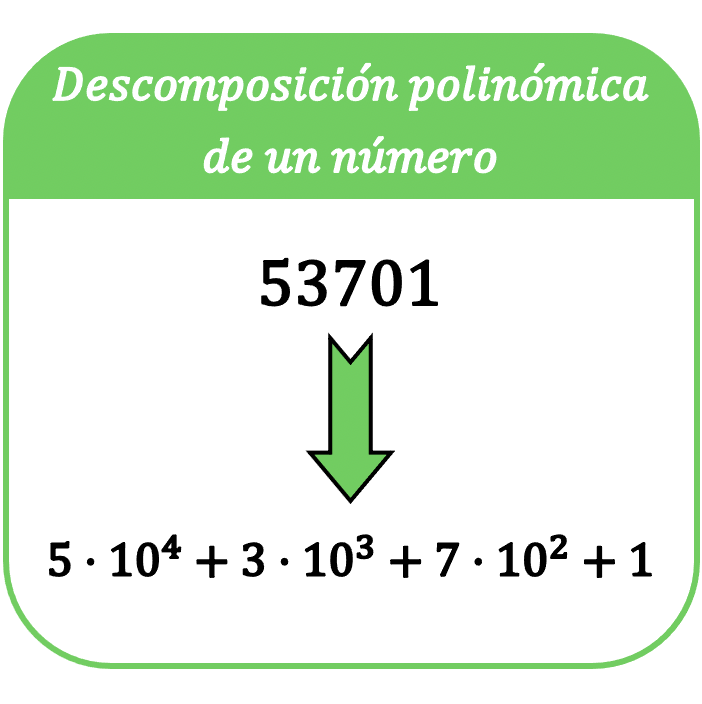
O termo decomposição polinomial de um número também é conhecido como expressão polinomial de um número .

Como fazer uma decomposição polinomial

Para realizar a decomposição polinomial de um número, você deve multiplicar cada dígito do número por 10 elevado ao número de dígitos à direita .

Por exemplo, se quisermos calcular a decomposição polinomial do seguinte número:

$86293$

Neste caso, o número 8 ocupa a quinta posição, portanto possui 4 dígitos à sua direita. Devemos, portanto, multiplicar oito por dez elevado a quatro:

$8\cdot 10^4$

Assim, para decompor polinomialmente o número 86293 você deve fazer o mesmo com todos os dígitos do número, e expressar todas as multiplicações na forma de uma soma:

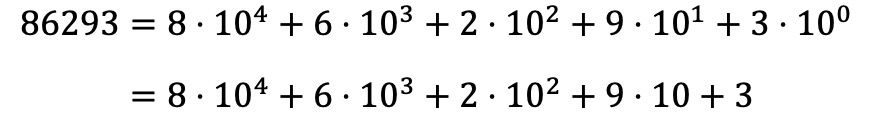
Observe que a potência 10 ⁰ desaparece porque, de acordo com as propriedades das potências, qualquer número elevado a 0 é igual a 1, então 10 ⁰ =1.

Por outro lado, você também pode encontrar a decomposição polinomial de um número a partir de sua decomposição multiplicativa:

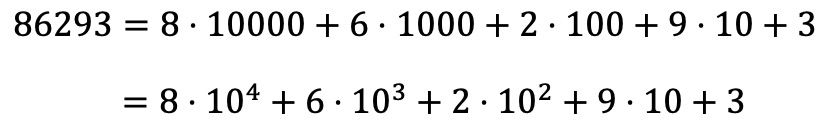
decomposição polinomial de números naturais para o ensino fundamental

Exemplos de decomposições polinomiais de números

Depois de vermos como se realiza a decomposição polinomial de um número, veremos diversos exemplos deste tipo de operação para compreender plenamente o conceito.

Decomposição polinomial de 3641:

$3641 = 3\cdot 10^3 +6 \cdot 10^2 + 4\cdot 10 + 1$

Decomposição polinomial de 56912:

$56912 = 5\cdot 10^4 +6\cdot 10^3 +9 \cdot 10^2 + 1\cdot 10 + 2$

Decomposição polinomial de 27084:

$\begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}$

Neste último exemplo, podemos simplificar a terceira multiplicação, pois qualquer número multiplicado por zero é anulado.

Decomposição polinomial de números decimais

Acabamos de ver como realizar a decomposição polinomial dos números naturais. Mas… como você decompõe um número decimal polinomialmente?

Pois bem, a decomposição polinomial com números decimais é feita da mesma forma que com os inteiros mas, além disso, somamos o produto de cada dígito decimal multiplicado por uma potência de base 10 cujo expoente é a posição decimal ocupada pelo referido algarismo com um negativo sinal.

Explicado em palavras isso pode parecer muito complicado, mas você verá que com um exemplo fica melhor compreendido:

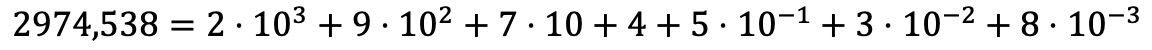
Exercícios resolvidos de decomposição polinomial

Para que você possa praticar decomposições polinomiais, preparamos diversos exercícios resolvidos passo a passo.

Não se esqueça que você pode nos tirar qualquer dúvida nos comentários! 🤔🤔🤔

Exercício 1

Execute a decomposição polinomial dos seguintes números:

$\text{A)} \ 7935$

$\text{B)} \ 1548$

$\text{C)} \ 55476$

$\text{D)} \ 287694$

Veja a solução

Para encontrar a decomposição polinomial de qualquer número, multiplique cada dígito desse número por 10 pelo número de dígitos à direita e, em seguida, some todas as multiplicações. Ainda:

$\text{A)} \ 7935 = 7 \cdot 10^3+ 9\cdot 10^2 +3 \cdot 10 +5$

$\text{B)} \ 1548 = 1 \cdot 10^3+ 5\cdot 10^2 +4 \cdot 10 +8$

$\text{C)} \ 55476 = 5\cdot 10^4+ 5 \cdot 10^3+ 4\cdot 10^2 +7\cdot 10 +6$

$\text{D)} \ 287694 = 2\cdot 10^5+8\cdot 10^4+ 7 \cdot 10^3+ 6\cdot 10^2 +9\cdot 10 +4$

Exercício 2

Encontre a decomposição polinomial dos seguintes números:

$\text{A)} \ 461$

$\text{B)} \ 3030$

$\text{C)} \ 11950$

$\text{D)} \ 8741866$

Veja a solução

Para decompor polinomialmente um número, você deve multiplicar cada dígito desse número por dez pelo número de dígitos à sua direita e, em seguida, adicionar todos os produtos. Ainda:

$\text{A)} \ 461 = 4\cdot 10^2 +6 \cdot 10 +1$

$\text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}$

$\text{C)} \ 11950 = 1\cdot 10^4+ 1 \cdot 10^3+ 9\cdot 10^2 +5\cdot 10$

$\text{D)} \ 8741866 = 8\cdot 10^6+7\cdot 10^5+4\cdot 10^4+ 1 \cdot 10^3+ 8\cdot 10^2 +6\cdot 10 +6$

Exercício 3

Calcule a decomposição polinomial dos seguintes números decimais:

$\text{A)} \ 51,63$

$\text{B)} \ 249,99$

$\text{C)} \ 0,82694$

$\text{D)} \ 5,7201$

Veja a solução

Neste problema todos os números são decimais, portanto para decompô-los você deve multiplicar cada dígito não decimal por 10 elevado ao número de dígitos que possui até a vírgula, e multiplicar cada dígito decimal por 10 elevado à sua posição decimal com um sinal negativo.

$\text{A)} \ 51,63 = 5 \cdot 10 +1 + 6 \cdot 10^{-1} +3 \cdot 10^{-2}$

$\text{B)} \ 249,99 = 2\cdot 10^2 + 4 \cdot 10 +9 + 9 \cdot 10^{-1} +9 \cdot 10^{-2}$

$\text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}$

$\text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}$

Decomposição polinomial (ou expressão) de um número

O que é decomposição polinomial de um número?

Como fazer uma decomposição polinomial

Exemplos de decomposições polinomiais de números

Decomposição polinomial de números decimais

Exercícios resolvidos de decomposição polinomial

Exercício 1

Exercício 2

Exercício 3

Deixe um comentário Cancelar resposta