▷ Composição de funções (ou função composta)

Neste artigo explicamos o que é a função composta (ou composição de funções). Além disso, você poderá ver vários exemplos de funções compostas e como é calculado o domínio deste tipo de funções. Por fim, você encontrará as propriedades da composição de funções e vários exercícios passo a passo para praticar.

O que é composição de funções?

A composição de funções consiste em avaliar sucessivamente o mesmo valor da variável independente (x) em duas ou mais funções. Por exemplo, compor as funções (gof)(x) dá a função composta g[f(x)].

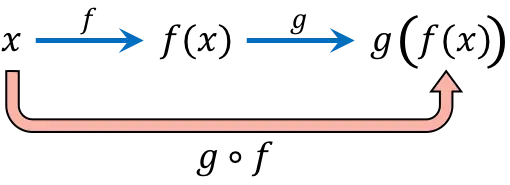
A expressão da função composta

$g\circ f$

lemos “f composto por g” ou “f seguido de g”.

Observe que a ordem é importante na composição da função, a função à direita do símbolo de composição é aplicada primeiro

$(f)$

então a função à esquerda do símbolo de composição

$(g).$

Exemplo de composição de função

Dada a definição de função composta, vejamos um exemplo de como calcular a composição de duas funções.

Dadas as duas funções diferentes a seguir:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Calcule a função composta

$\left(g \circ f\right)(x)$

e avaliá-lo em

$x=3.$

A composição das funções

$\left(g \circ f\right)(x)$

Isso significa que precisamos executar a seguinte função composta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Para resolver isso, substituímos

$f(x)$

por sua expressão algébrica:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

E agora tomamos a função de

$g(x)=\cfrac{x+4}{2}$

e colocamos a expressão

$3x+1$

onde há um

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Desta forma já calculamos a função f composta por g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Finalmente, para avaliar a função composta em

$x=3$

Basta calcular a imagem da função nesse valor:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Domínio de função composta

Normalmente, quando realizamos operações sobre funções, o domínio da função resultante é a intersecção dos domínios das funções originais. No entanto, esta propriedade não é satisfeita pela composição de funções.

O domínio da composição de funções

$(g\circ f)(x)$

é equivalente ao conjunto de todos os valores de x no domínio da função

$f$

como

$f(x)$

pertence ao domínio da função

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Portanto, para calcular o domínio de uma função composta, você deve primeiro encontrar o domínio de cada função separadamente e depois o domínio da função resultante da operação. Assim, o domínio de composição das funções será composto por todos os valores que satisfaçam a condição matemática anterior.

👉 Lembre-se, se você encontrar um problema que não sabe resolver, pode nos perguntar nos comentários abaixo!

Propriedades da composição de funções

As funções compostas possuem as seguintes características:

A composição de funções possui propriedade associativa, portanto, a seguinte equação é sempre verdadeira:

$f\circ (g\circ h)=(f\circ g)\circ h$

Em geral, a composição da função não é comutativa, portanto a ordem da operação determina o resultado:

$f\circ g\neq g\circ f$

O elemento neutro da composição de funções corresponde à função identidade
$f(x)=x.$

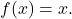
Assim, qualquer função composta com a função identidade resulta na própria função:

$f\circ id = id \circ f = f$

$id = x$

Calcular o inverso da composição de duas funções equivale a primeiro encontrar o inverso de cada função e depois determinar a função composta:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

A função inversa também atua como elemento simétrico da função composta, pois a composição de uma função com sua inversa é equivalente à função identidade:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

A derivada da composição de duas funções é calculada usando a regra da cadeia:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Veja: qual é a regra da cadeia?

Exercícios resolvidos sobre composição de funções

Exercício 1

Dadas as duas funções a seguir:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Calcule as composições das funções f composta por g e g composta por f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Veja a solução

A composição das funções

$\left(g \circ f\right)(x)$

significa calcular a seguinte função composta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Então, para resolver isso, substituímos

$f(x)$

pela sua expressão:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

Isto significa que na expressão de

$g(x) =5x+4$

você precisa substituir a variável

$x$

Para

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Ainda:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Por outro lado, para encontrar a função g composta por f você deve fazer o mesmo procedimento mas com a ordem inversa:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Este exercício também demonstra a propriedade de que funções compostas não são comutativas, pois o resultado depende da ordem em que as funções são aplicadas.

Exercício 2

Dadas as duas funções a seguir:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Calcula a composição de funções f compostas com g .

$(g\circ f)(x)$

Veja a solução

A função f composta por g significa resolver a seguinte função composta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Portanto, substituímos a função f(x) pela sua expressão:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

E agora temos que substituir

$x$

Para

$x^2-3$

na expressão da função g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Resumindo, o resultado da composição de funções é:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Exercício 3

Dadas as duas funções quadráticas a seguir:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Determine o resultado da seguinte composição de funções:

$(g\circ f)(2)$

Veja a solução

$\left(g \circ f\right)(2)$

consiste em encontrar a seguinte função composta:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Então, para resolver a função composta, primeiro calculamos

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Portanto, como

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Então, para encontrar o valor da função composta basta calcular

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Em resumo, o resultado do problema de composição de funções é:

$\bm{\left(g \circ f\right)(2) =8}$

Exercício 4

Dadas as duas funções a seguir:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Encontre o resultado de g composto por f em x=2:

$(f\circ g)(2)$

Veja a solução

Neste caso, devemos calcular a seguinte função composta:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Então primeiro encontramos

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

E então, tipo

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Então, para resolver a função composta, precisamos calcular

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$