Como diagonalizar uma matriz

Nesta página você encontrará tudo sobre matrizes diagonalizáveis: o que são, quando podem ser diagonalizadas e quando não podem, o método para diagonalizar matrizes, as aplicações e propriedades dessas matrizes específicas, etc. E você ainda tem vários exercícios resolvidos passo a passo para praticar e entender perfeitamente como eles são diagonalizados. Por fim, aprendemos também como realizar diagonalizações de matrizes com o programa de computador MATLAB, já que é muito utilizado.

O que é uma matriz diagonalizável?

Como veremos a seguir, diagonalizar uma matriz é muito útil no campo da álgebra linear. É por isso que muitos perguntam… o que é diagonalização de matrizes? Bem, a definição de uma matriz diagonalizável é:

Uma matriz diagonalizável é uma matriz quadrada que pode ser transformada em uma matriz diagonal, ou seja, uma matriz preenchida com zeros exceto na diagonal principal. A diagonalização das matrizes é dividida da seguinte forma:

$A = PDP^{-1}$

Ou equivalente,

$D = P^{-1}AP$

Ouro

$A$

é a matriz a ser diagonalizada,

$P$

é a matriz cujas colunas são os autovetores (ou autovetores) de

$A$

$P^{-1}$

sua matriz inversa e

$D$

é a matriz diagonal formada pelos autovalores (ou autovalores) de

$A$

O Matrix

$P$

atua como uma base muda a matriz, então na verdade com esta fórmula mudamos a base para a matriz

$A$

, de modo que a matriz se torna uma matriz diagonal (

$D$

) na nova base.

Portanto, a matriz

$A$

e a matriz

$D$

São matrizes semelhantes. E obviamente,

$P$

É uma matriz regular ou não degenerada.

Quando você pode diagonalizar uma matriz?

Nem todas as matrizes podem ser diagonalizadas; apenas matrizes que atendam a certas características podem ser diagonalizadas. Você pode saber se uma matriz é diagonalizável de diferentes maneiras:

Uma matriz quadrada de ordem n é diagonalizável se tiver n autovetores (ou autovetores) linearmente independentes , ou em outras palavras, se esses vetores formarem uma base. Isso ocorre porque a matriz
$P$

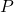
, que serve para diagonalizar uma matriz, é formado pelos autovetores dessa matriz. Para saber se os autovetores são LI, basta que o determinante da matriz

$P$

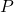
é diferente de 0, o que significa que a matriz tem a classificação máxima.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Uma propriedade dos autovalores e autovetores é que os autovetores de diferentes autovalores são linearmente independentes. Portanto, se todos os autovalores da matriz forem únicos, a matriz é diagonalizável.

Outra forma de determinar se uma matriz pode ser acomodada em uma matriz diagonal é usar multiplicidades algébricas e geométricas. A multiplicidade algébrica é o número de vezes que um autovalor (ou autovalor) é repetido, e a multiplicidade geométrica é a dimensão do núcleo (ou núcleo) da matriz subtraindo o autovalor em sua diagonal principal. Assim, se para cada autovalor a multiplicidade algébrica for igual à multiplicidade geométrica , a matriz é diagonalizável.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Por fim, existe um teorema, o teorema espectral, que garante a diagonalização de matrizes simétricas com números reais. Em outras palavras, qualquer matriz real e simétrica é diagonalizável .

Como diagonalizar uma matriz

O procedimento para diagonalizar uma matriz é baseado em encontrar os autovalores (ou autovalores) e autovetores (ou autovetores) de uma matriz. É por isso que é importante que você domine como calcular os autovalores (ou autovalores) e autovetores (ou autovetores) de qualquer matriz . Você pode relembrar como foi feito clicando no link, onde explicamos passo a passo como encontrá-los e alguns truques que facilitam muito os cálculos. Além disso, você também encontrará exercícios resolvidos para praticar.

Com o método a seguir, você pode diagonalizar uma matriz de qualquer dimensão: 2×2, 3×3, 4×4, etc. As etapas a seguir para diagonalizar uma matriz são:

Obtenha os autovalores (ou autovalores) da matriz.
Calcule o autovetor associado a cada autovalor.
Construa a matriz
$P$

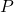
, cujas colunas são os autovetores da matriz a ser diagonalizada.
Verifique se a matriz pode ser diagonalizada (deve atender a uma das condições explicadas na seção anterior).
Construa a matriz diagonal
$D$

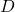
, cujos elementos são todos 0, exceto aqueles na diagonal principal, que são os autovalores encontrados na etapa 1.

Aviso: Os autovetores da matriz

$P$

podem ser colocados em qualquer ordem, mas os autovalores da matriz diagonal

$D$

Eles devem ser colocados na mesma ordem. Por exemplo, o primeiro autovalor da matriz diagonal

$D$

deve ser aquele que corresponde ao autovetor da primeira coluna da matriz

$P$

Abaixo estão vários exercícios passo a passo de diagonalização de matrizes que você pode praticar.

Exercícios de diagonalização de matrizes resolvidos

Exercício 1

Diagonalize a seguinte matriz quadrada de dimensão 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Veja a solução

Devemos primeiro determinar os autovalores da matriz A. Portanto, calculamos a equação característica resolvendo o seguinte determinante:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Agora vamos calcular as raízes do polinômio característico:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Uma vez obtidos os autovalores, calculamos o autovetor associado a cada um. Primeiro, o autovetor correspondente ao autovalor 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

E então calculamos o autovetor associado ao autovalor 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Nós construímos a matriz

$P$

, formado pelos autovetores da matriz:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Como todos os autovalores são diferentes, a matriz A é diagonalizável. Assim a matriz diagonal correspondente é aquela que possui os autovalores na diagonal principal:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Lembre-se de que os autovalores devem ser colocados na mesma ordem em que os autovetores são colocados na matriz

$P$

Concluindo, a matriz de mudança de base e a matriz diagonalizada são:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Exercício 2

Diagonalize a seguinte matriz quadrada de ordem 2:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Veja a solução

Devemos primeiro determinar os autovalores da matriz A. Portanto, calculamos a equação característica resolvendo o seguinte determinante:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Agora vamos calcular as raízes do polinômio característico:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Uma vez obtidos os autovalores, calculamos o autovetor associado a cada um. Primeiro, o autovetor correspondente ao autovalor -1:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

E então calculamos o autovetor associado ao autovalor 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Nós construímos a matriz

$P$

, formado pelos autovetores da matriz:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Como todos os autovalores são diferentes entre si, a matriz A é diagonalizável. Assim, a matriz diagonal correspondente é aquela que contém os autovalores na diagonal principal:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Lembre-se de que os autovalores devem ser colocados na mesma ordem em que os autovetores são colocados na matriz

$P$

Concluindo, a matriz de mudança de base e a matriz diagonalizada são:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Exercício 3

Diagonalize a seguinte matriz quadrada de dimensão 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Veja a solução

O primeiro passo consiste em encontrar os autovalores da matriz A. Calculamos, portanto, a equação característica resolvendo o determinante da seguinte matriz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Devemos agora calcular as raízes do polinômio característico. Por se tratar de um polinômio de terceiro grau, aplicamos a regra de Ruffini:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

E então encontramos as raízes do polinômio obtido:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Portanto, os autovalores da matriz são:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Uma vez encontrados os autovalores, calculamos o autovetor associado a cada um deles. Primeiro, o autovetor correspondente ao autovalor 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Em seguida, calculamos o autovetor associado ao autovalor 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

E por fim, calculamos o autovetor associado ao autovalor 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Nós construímos a matriz

$P$

, formado pelos autovetores da matriz:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Como todos os autovalores são diferentes entre si, a matriz A é diagonalizável. Assim a matriz diagonal correspondente é aquela que possui os autovalores na diagonal principal:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Lembre-se de que os autovalores devem ser colocados na mesma ordem em que os autovetores são colocados na matriz

$P$

Resumindo, a matriz de mudança de base e a matriz diagonalizada são:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Exercício 4

Diagonalize, se possível, a seguinte matriz quadrada de ordem 3:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Veja a solução

O primeiro passo consiste em encontrar os autovalores da matriz A. Calculamos, portanto, a equação característica resolvendo o determinante da seguinte matriz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Devemos agora calcular as raízes do polinômio mínimo. Por se tratar de um polinômio de terceiro grau, aplicamos a regra de Ruffini para fatorá-lo:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

E então encontramos as raízes do polinômio obtido:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Portanto, os autovalores da matriz são:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

O autovalor de -2 é de multiplicidade algébrica simples, por outro lado o autovalor de 2 é de dupla multiplicidade.

Uma vez encontrados os autovalores, calculamos o autovetor associado a cada um deles. Primeiro, o autovetor correspondente ao autovalor -2:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Vamos agora calcular os autovetores associados aos autovalores 2.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Como o autovalor 2 é repetido duas vezes, precisamos calcular outro autovetor que satisfaça as equações do subespaço (ou autoespaço):

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Nós construímos a matriz

$P$

, formado pelos três autovetores da matriz:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

No entanto, os três vetores não são linearmente independentes, uma vez que obviamente os dois autovetores com autovalor 2 são uma combinação linear um do outro. Isso também pode ser demonstrado porque o determinante da matriz

$P$

é igual a 0 (tem uma linha cheia de zeros):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Portanto, como os autovetores são linearmente dependentes, a matriz A não é diagonalizável .

Exercício 5

Se possível, diagonalize a seguinte matriz quadrada de tamanho 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Veja a solução

O primeiro passo consiste em encontrar os autovalores da matriz A. Calculamos, portanto, a equação característica resolvendo o determinante da seguinte matriz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Como a primeira linha é inteiramente composta por zeros exceto 3, aproveitaremos isso para resolver o determinante da matriz por cofatores (ou adjuntos):

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Agora precisamos calcular as raízes do polinômio característico. É melhor não multiplicar os parênteses porque obteria um polinômio de terceiro grau. Por outro lado, se os dois fatores forem resolvidos separadamente, é mais fácil obter os autovalores:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Portanto, os autovalores da matriz são:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Uma vez encontrados os autovalores, calculamos o autovetor associado a cada um deles. Primeiro, o autovetor correspondente ao autovalor 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Em seguida, calculamos os autovetores associados aos autovalores 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Como o autovalor 3 é repetido duas vezes, precisamos calcular outro autovetor que satisfaça as equações do autoespaço:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Nós construímos a matriz

$P$

, formado pelos autovetores da matriz:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

Ao contrário do exercício 4, neste caso conseguimos formar 3 vetores linearmente independentes embora a multiplicidade algébrica do autovalor 3 seja dupla. Isso pode ser verificado vendo que o determinante da matriz

$P$

dá um resultado diferente de 0:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

Podemos assim realizar a decomposição diagonal da matriz A. E a matriz diagonal correspondente é aquela que possui os autovalores na diagonal principal:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Lembre-se de que os autovalores devem ser colocados na mesma ordem em que os autovetores são colocados na matriz

$P$

Resumindo, a matriz de mudança de base necessária para diagonalizar a matriz e sua forma diagonalizada são:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Exercício 6

Faça a diagonalização, se possível, da seguinte matriz de dimensão 4×4:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Veja a solução

O primeiro passo consiste em encontrar os autovalores da matriz A. Calculamos, portanto, a equação característica resolvendo o determinante da seguinte matriz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

Neste caso, a última coluna do determinante é composta apenas por zeros exceto um elemento, portanto aproveitaremos isso para calcular o determinante por cofatores através desta coluna:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Devemos agora calcular as raízes do polinômio característico. É melhor não fazer o produto dos parênteses porque assim obteria um polinômio de quarto grau. Porém, se os dois fatores forem resolvidos separadamente, é mais fácil calcular os autovalores:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Portanto, os autovalores da matriz são:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Uma vez encontrados todos os autovalores, avançamos em direção aos autovetores. Calculamos o autovetor associado ao autovalor 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calculamos o autovetor associado ao autovalor -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calculamos o autovetor associado ao autovalor 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calculamos o autovetor associado ao autovalor 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Nós fazemos a matriz

$P$

, composto pelos autovetores da matriz:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

Como todos os autovalores são diferentes entre si, a matriz A é diagonalizável. Assim a matriz diagonal correspondente é aquela que possui os autovalores na diagonal principal:

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Lembre-se que os autovalores devem ser colocados na mesma ordem em que os autovetores estão posicionados na matriz

$P$

Em resumo, as mudanças básicas de matriz necessárias para diagonalizar a matriz A e a matriz na forma diagonal são:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Aplicações de matrizes diagonalizáveis

Se você chegou até aqui, provavelmente está se perguntando: para que serve uma matriz diagonalizável?

Bem, matrizes diagonalizáveis são muito úteis e amplamente utilizadas em matemática. A razão é que uma matriz diagonal está praticamente cheia de zeros e, portanto, facilita muito os cálculos.

Um exemplo claro disso são as potências de matrizes diagonalizáveis, pois seu resultado é simplificado pela seguinte fórmula:

$\displaystyle A^k=PD^kP^{-1}$

Esta igualdade pode ser facilmente comprovada por indução. É, portanto, suficiente elevar a matriz

$D$

ao expositor. E por se tratar de uma matriz diagonal, a operação se resume a elevar cada termo da diagonal principal ao expoente:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Exemplo de potência de uma matriz diagonalizável

Para entender melhor, calcularemos a potência de uma matriz diagonalizável como exemplo:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

A Matriz Básica de Mudança

$P$

, formado por seus autovetores, e a matriz diagonalizada

$D$

, compostos por valores próprios, são:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Então, para dar um exemplo, a matriz A elevada a 7 é equivalente a:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Agora invertemos a matriz

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Resolvemos a potência da matriz

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

E, por fim, realizamos as multiplicações das matrizes:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Como você viu, é mais conveniente calcular a potência com uma matriz diagonal do que multiplicar a mesma matriz sete vezes seguidas. Então imagine com valores de expoentes muito maiores.

Propriedades de matrizes diagonalizáveis

As características deste tipo de matriz são:

Se a matriz
$A$

é diagonalizável, qualquer potência de

$A$

.

Quase todas as matrizes podem ser diagonalizadas em um ambiente complexo
$\mathbb{C}$

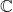
. Embora abaixo você tenha as exceções que nunca são diagonalizáveis.

Se a matriz
$P$

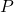
é uma matriz ortogonal, então dizemos que a matriz

$A$

é ortogonalmente diagonalizável e, portanto, a equação pode ser reescrita:

$\displaystyle A=PDP^t$

Uma matriz é diagonalizável por uma matriz unitária se e somente se for uma matriz normal.

Dadas duas matrizes diagonalizáveis, elas são comutáveis se e somente se puderem ser diagonalizadas simultaneamente, ou seja, se compartilharem a mesma base ortonormal de autovetores (ou autovetores).

Se um endomorfismo é diagonalizável, dizemos que é diagonalizável por similaridade . Porém, nem todos os endomorfismos são diagonalizáveis, ou seja, a diagonalização de um endomorfismo não é garantida.

Diagonalização Simultânea

Diz-se que um conjunto de matrizes é simultaneamente diagonalizável se existir uma matriz invertível que sirva de base para diagonalizar qualquer matriz deste conjunto. Em outras palavras, se duas matrizes diagonalizam na mesma base de autovetores, isso significa que elas são diagonalizáveis simultaneamente.

Além disso, como comentamos nas propriedades da diagonalização de matrizes, se duas matrizes são capazes de diagonalizar simultaneamente, elas devem comutar entre si.

Por exemplo, as duas matrizes a seguir são comutáveis, portanto elas diagonalizam na mesma base de autovetores ou autovetores.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Mesmo que tenham os mesmos autovetores, isso não significa que tenham os mesmos autovalores. Na verdade, embora as matrizes A e B acima tenham autovetores semelhantes, elas têm autovalores diferentes.

Matrizes não diagonalizáveis

Embora a grande maioria das matrizes seja diagonalizável em um ambiente de números complexos, algumas matrizes nunca podem ser diagonalizadas.

Este fato ocorre quando a multiplicidade algébrica de um autovalor (ou autovalor) não coincide com a multiplicidade geométrica.

Por exemplo, a seguinte matriz não pode ser diagonalizada de forma alguma, ela é “indiagonalizável”:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Além disso, existem matrizes que não são capazes de diagonalizar em um ambiente de números reais, mas diagonalizam ao trabalhar com números complexos, como esta matriz:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Finalmente, existem alguns procedimentos de diagonalização de blocos de matrizes que não são puramente diagonalizáveis, mas são um pouco mais complicados. O método mais conhecido é a diagonalização com a forma canônica de Jordan .

Diagonalize uma matriz com MATLAB

Os programas de computador são muito úteis quando se trata de diagonalizar matrizes, especialmente se forem muito grandes. E o software mais conhecido é certamente MATLAB , então a seguir veremos como fatorar diagonalmente uma matriz usando este programa.

A instrução usada para diagonalizar uma matriz com MATLAB é:

$\displaystyle \text{[P, D] = eig(A)}$

Ouro

$A$

é a matriz a ser diagonalizada e

$P$

$D$

são as matrizes que o programa retorna:

$P$

é a matriz formada pelos autovetores e

$D$

é a matriz em forma diagonal cujos principais termos diagonais são os autovalores.

Portanto, você só precisa inserir este código no programa.

Por outro lado, se você quiser apenas saber os autovalores, poderá usar a seguinte instrução:

$\displaystyle e= eig(A)}$

Ouro

$e$

é o vetor coluna que o MATLAB retorna com os autovalores da matriz

$A$

O que é uma matriz diagonalizável?

Quando você pode diagonalizar uma matriz?

Como diagonalizar uma matriz

Exercícios de diagonalização de matrizes resolvidos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Aplicações de matrizes diagonalizáveis

Exemplo de potência de uma matriz diagonalizável

Propriedades de matrizes diagonalizáveis

Diagonalização Simultânea

Matrizes não diagonalizáveis

Diagonalize uma matriz com MATLAB

Deixe um comentário Cancelar resposta