Combinação linear de vetores -

Nesta página você encontrará a explicação do que significa uma combinação linear entre vetores. Além disso, você poderá ver um exemplo de como um vetor é expresso como uma combinação linear e, além disso, poderá praticar com exercícios e problemas resolvidos passo a passo.

O que é combinação linear de vetores?

A definição de combinação linear é a seguinte:

Uma combinação linear de um conjunto de vetores é o vetor obtido pela soma de todos os vetores do conjunto multiplicado por escalares (números reais).

Em outras palavras, dado um conjunto de vetores

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

uma combinação linear deles seria:

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

Onde os coeficientes

$a_i$

Estes são números reais.

Portanto, um vetor que é uma combinação linear de outros vetores significa que o primeiro pode ser expresso em termos do segundo.

Este conceito pode ser melhor compreendido representando graficamente um vetor no plano que é uma combinação linear de dois vetores:

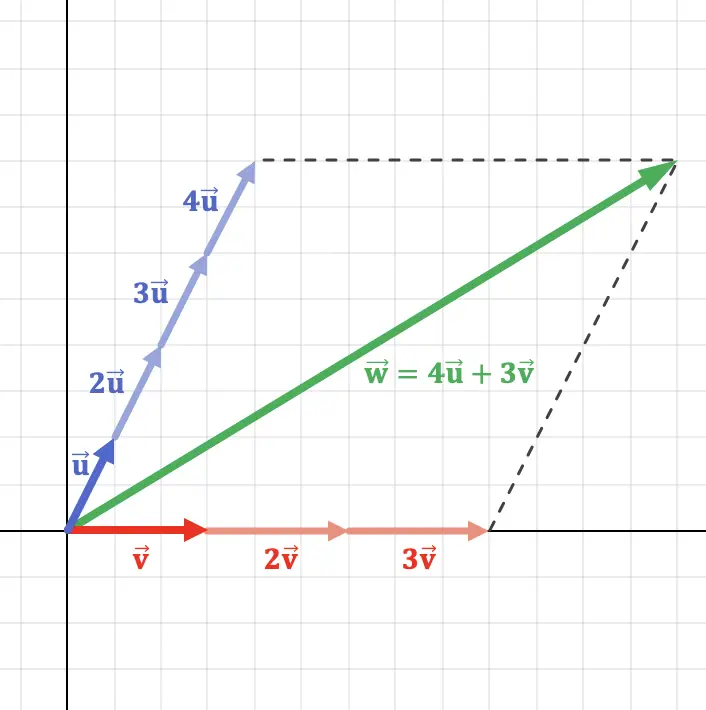
Como você pode ver na representação gráfica acima, o vetor

$\vv{\text{w}}$

pode ser obtido a partir de vetores

$\vv{\text{u}}$

$\vv{\text{v}}$

realizar operações vetoriais. Portanto, o vetor

$\vv{\text{w}}$

é uma combinação linear dos outros dois vetores.

Deve-se ressaltar que esta combinação linear é única , ou seja, existe apenas uma combinação linear viável para cada vetor. Visto que, seguindo o exemplo anterior, se multiplicarmos

$\vv{\text{u}}$

para 6 em vez de 4, obteríamos outro vetor diferente.

Além disso, uma das propriedades da combinação linear no plano (em R2) é que qualquer vetor pode ser colocado como uma combinação linear de dois outros vetores se eles tiverem direções diferentes, ou seja, se não forem paralelos.

Além disso, às vezes podemos identificar a olho nu que dois vetores são uma combinação linear. Para isso, basta que seus componentes sejam proporcionais . Por exemplo, as coordenadas dos dois vetores a seguir são proporcionais e, portanto, os vetores são uma combinação linear:

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Finalmente, seja num espaço vetorial bidimensional (em R2) ou tridimensional (em R3), se existir uma combinação linear dentro de um conjunto de vetores, isso implica que eles são linearmente dependentes uns dos outros. Por outro lado, se nenhuma combinação linear for possível entre os vetores, isso significa que eles são linearmente independentes .

Se este último conceito não estiver totalmente claro para você, recomendamos conferir nossa explicação sobre vetores linearmente dependentes e independentes , aqui você encontrará o que significa vetores serem linearmente dependentes ou independentes, exemplos de cada tipo e as diferenças entre eles. . Esse conceito é muito utilizado e, de fato, é muito questionado nas provas, por isso é importante que você o entenda bem.

Como expressar um vetor como uma combinação linear de outros vetores

Veremos então como resolver um problema típico em que somos solicitados a determinar a combinação linear de um vetor.

Expresse o vetor
$\vv{\text{x}}$

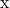
como uma combinação linear de

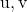
$\vv{\text{u}}, \vv{\text{v}}$

E

$\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

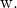
Para que o vetor

$\vv{\text{x}}$

ser uma combinação linear dos outros vetores, a seguinte equação deve ser cumprida:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Onde os coeficientes

$a_1, a_2$

$a_3$

Estas são as incógnitas que devemos encontrar.

Portanto, substituímos cada vetor por suas coordenadas:

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

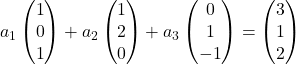
Multiplicamos cada vetor pelo seu coeficiente:

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

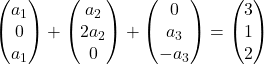
Adicionamos vetores:

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

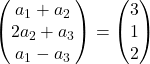
Cada coordenada esquerda deve ser igual a cada coordenada direita. Temos, portanto, 3 equações:

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

Resta resolver o sistema de equações obtido. Para isso, utilize o método de sua preferência (método de substituição, regra de Cramer, método de Gauss-Jordan, etc.), neste caso utilizaremos o método de Gauss:

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

O sistema de etapas obtido é portanto:

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

Tudo o que precisamos fazer agora é esclarecer as incógnitas e descobrir o seu valor. Então, da última equação encontramos

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

A partir da segunda equação do sistema, calculamos o valor de

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

E finalmente, a partir da primeira equação do sistema de etapas, encontramos a incógnita

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

A solução do sistema de equações lineares é, portanto:

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

Então o vetor

$\vv{\text{x}}$

Pode ser expresso pela seguinte combinação linear:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

Existe, portanto, efetivamente uma dependência linear entre os vetores. Por outro lado, se nenhuma solução do sistema de equações tivesse sido obtida, isso significaria que o vetor

$\vv{\text{x}}$

É linearmente independente em relação aos demais vetores e, portanto, não haveria combinação linear possível para obter o referido vetor a partir dos demais vetores.

Exercícios resolvidos sobre combinação linear de vetores

Exercício 1

Entre os três vetores a seguir, indique quais pares são combinações lineares entre si. Além disso, encontre a relação de combinação linear dos referidos pares de vetores.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

Veja a solução

Para saber se um par de vetores é uma combinação linear, devemos ver se suas coordenadas são proporcionais.

Primeiro verificamos o vetor

$\vv{\text{u}}$

com o vetor

$\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

Em segundo lugar, verificamos o vetor

$\vv{\text{u}}$

com o vetor

$\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

Finalmente, testamos o vetor

$\vv{\text{v}}$

com o vetor

$\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Portanto, o único par de vetores que são combinações lineares é

$\vv{\text{v}}$

$\vv{\text{w}}.$

Além disso, a relação deles é a seguinte:

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

Ou equivalente:

$\vv{\text{w}}= -3 \vv{\text{v}}$

Embora a declaração não exija isso, os únicos vetores que dependem linearmente uns dos outros são

$\vv{\text{v}}$

$\vv{\text{w}}$

porque existe uma combinação linear entre eles. Os outros pares são linearmente independentes porque não podem ser combinados linearmente.

Exercício 2

Encontre a relação linear entre o vetor

$\vv{\text{x}}$

e o conjunto de vetores

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

Veja a solução

Para que o vetor

$\vv{\text{x}}$

ser uma combinação linear dos outros vetores, a seguinte equação deve ser cumprida:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Portanto, substituímos cada vetor por suas coordenadas:

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

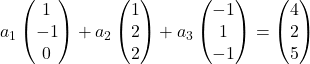
Multiplicamos cada vetor por sua constante:

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

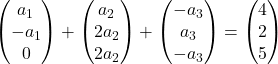
Adicionamos os vetores:

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

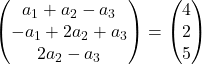
Obtemos, portanto, o seguinte sistema de equações:

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

Resolvemos o sistema obtido pelo método de Gauss:

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

O sistema de etapas obtido é portanto:

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

Tudo o que precisamos fazer agora é esclarecer as incógnitas e descobrir o seu valor. Então, da última equação encontramos

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

A partir da segunda equação do sistema, calculamos o valor de

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

E finalmente, a partir da primeira equação do sistema de etapas, encontramos a incógnita

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

A solução do sistema de equações lineares é, portanto:

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

Então o vetor

$\vv{\text{x}}$

Pode ser expresso pela seguinte combinação linear:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

Exercício 3

Expresse o vetor

$\vv{\text{x}}$

como uma combinação linear de vetores

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

Veja a solução

Propomos a equação de combinação linear em relação ao vetor

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Portanto, substituímos cada vetor por seus componentes:

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

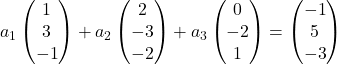
Multiplicamos cada vetor por sua respectiva incógnita:

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

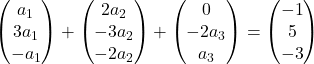
Realizamos a adição de vetores:

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

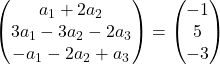
Obtivemos, portanto, o seguinte sistema de equações:

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

Resolvemos o sistema obtido pelo método de Gauss:

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

O sistema de etapas obtido é portanto:

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

Tudo o que precisamos fazer agora é esclarecer as incógnitas e descobrir o seu valor. Então, da última equação encontramos

$a_3:$

$a_3 = -4$

A partir da segunda equação do sistema, encontramos o valor de

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

E finalmente, a partir da primeira equação do sistema de etapas, resolvemos a incógnita

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

A solução do sistema de equações lineares é, portanto:

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

Então o vetor

$\vv{\text{x}}$

pode ser expresso combinando linearmente os outros vetores:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

Exercício 4

Determine se o vetor

$\vv{\text{x}}$

pode ser expresso como uma combinação linear dos vetores

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

Neste caso, encontre a expressão que os conecta.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

Veja a solução

Para que o vetor

$\vv{\text{x}}$

ser uma combinação linear dos outros vetores, a seguinte equação deve ser cumprida:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Portanto, substituímos cada vetor por suas coordenadas:

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

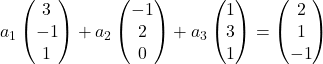
Multiplicamos cada vetor pelo seu coeficiente:

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

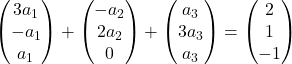
Adicionamos os vetores:

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

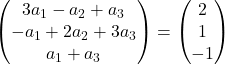
A expressão anterior é, portanto, equivalente ao seguinte sistema de equações:

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

Resolvemos agora o sistema obtido pelo método de Gauss:

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

Obtivemos, portanto, o seguinte sistema de equações:

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

Porém, a última equação nunca poderá ser cumprida, pois 0 nunca será igual a -30 quaisquer que sejam os valores que as incógnitas assumam. Portanto, o sistema não tem solução e isso implica que não existe combinação linear para calcular o vetor

$\vv{\text{x}}.$

O que é combinação linear de vetores?

Como expressar um vetor como uma combinação linear de outros vetores

Exercícios resolvidos sobre combinação linear de vetores

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta