Calcule o mínimo múltiplo comum (lcm)

O mínimo múltiplo comum (MCM) de dois ou mais números é o menor múltiplo (diferente de zero) que esses números têm em comum. É a operação inversa do máximo divisor comum , embora seja calculada utilizando métodos semelhantes. Se você deseja aprender como calcular o MMC, recomendamos que continue lendo, pois neste artigo explicaremos todos os procedimentos (do mais simples ao mais complicado) para encontrar o menor múltiplo comum de um conjunto de números.

calculadora lcm

Antes de começarmos a falar sobre como obter lcm, queremos que você saiba que nesta página temos uma calculadora múltipla mínima comum . Com ele você poderá calcular o lcm de todos os números que desejar, desta forma poderá comparar os resultados dos seus exercícios para ver se os resolveu corretamente.

Para usar a calculadora múltipla menos comum, insira números inteiros separados por vírgula:

calcular lcm

Como calcular o mínimo múltiplo comum?

Para encontrar o mínimo múltiplo comum de dois ou mais números, você precisa seguir um dos três métodos que explicaremos a seguir. A seguir, ao detalharmos cada um dos procedimentos que você pode escolher, também lhe diremos quais são suas vantagens e desvantagens. Assim você saberá qual escolher em cada situação para resolver de forma fácil e rápida o LCM em questão.

Método 1: lista múltipla

O primeiro método é criar uma lista de múltiplos dos números que deseja calcular no LCM. Depois você precisa encontrar o menor valor que se repete em todas as listas , desta forma você terá o menor múltiplo comum. Então veremos com um exemplo: lcm (5, 6).

Método 2: decomposição fatorial

Em segundo lugar, podemos optar por fatorar os números. Mais especificamente, este método facilitará o cálculo do pcm de números grandes . Já que seguir o método 1 ao executar lcm de números grandes pode ser lento e tedioso, simplesmente porque teremos que escrever listas muito longas de múltiplos. Este segundo procedimento pode ser um pouco mais complicado de entender no início, mas quando você entende a mecânica ele tem muitas vantagens em relação ao anterior. Dito isso, vamos ver o procedimento a seguir:

• Decomposição fatorial: o primeiro passo será decompor todos os números que vamos incluir no MMC em fatores primos. Caso você não saiba como decompor um número fatorialmente , recomendamos entrar neste último link, lá você encontrará uma explicação de primeira classe sobre como simplificar números de forma rápida e eficiente.
• Crie uma única expressão matemática: Quando tivermos todos os números expressos como fatores primos, escolheremos os números comuns e não comuns elevados ao maior expoente. Depois você os escreve como uma única expressão matemática e finalmente resolve as multiplicações e/ou potências necessárias. E você já terá o valor numérico de lcm.

Método 3: fórmula matemática

Existe uma forma final de obter o mínimo múltiplo comum, que consiste em utilizar o MDC e a seguinte fórmula matemática:

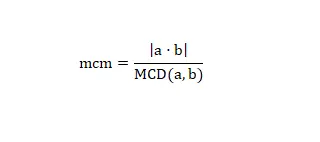
Usando esta fórmula podemos calcular o lcm de qualquer número. Vejamos um exemplo real, se quisermos calcular lcm (2,6) basta resolver a operação (2 x 6) / 2 = 6. E já teremos resolvido o cálculo, como vocês podem ver é um método simples e rápido se você tiver o GCD ou puder calculá-lo facilmente.

Dicas para calcular lcm rapidamente

Depois de dominar os três métodos que acabamos de explicar, recomendamos que você leia as propriedades do mínimo múltiplo comum sobre as quais falaremos agora. Pois graças a eles você poderá identificar algumas situações específicas em que o LCM pode ser calculado muito rapidamente, sem a necessidade de utilizar as estratégias já explicadas.

• Primeiro número divisível pelo segundo: se quisermos calcular o menor múltiplo comum de aeb quando a divide b, então o ppcm desses dois números será o maior (neste caso b). Por exemplo, se quiser calcular o lcm de 2 e 8, o resultado será o maior, portanto 8.
• Dois números primos: No caso de encontrar dois números primos , o método mais rápido é multiplicá-los e o resultado será o ppcm. Isso é lógico, pois seu máximo divisor comum é 1, o que significa que não conseguiremos decompor o número em fatores mais simples que o próprio número e, portanto, só conseguiremos multiplicá-los entre si. Por exemplo, o MMC de 3 e 5 será o resultado do seu produto: 3 x 5 = 15.

Como obter o mínimo múltiplo comum em frações?

Quando queremos resolver uma adição ou subtração de frações, precisamos calcular o menor denominador comum, que é igual a lcm, mas aplicado a frações. Basicamente, procuramos o lcm dos dois denominadores para que possamos então expressar a soma como uma única fração. Se você quiser ver como o menor denominador comum é aplicado a um cálculo de fração real, você pode entrar neste link .

Lcm na calculadora científica

A tecla LCM, encontrada em qualquer calculadora científica, permite calcular o menor múltiplo comum de dois números inteiros. No caso das calculadoras Casio, a sintaxe ou procedimento que você precisa seguir é o seguinte. Primeiro, você pressiona APHA + MCM (esta última tecla será rotulada em marrom). Feito isso, você pode inserir os dois números, mas lembre-se que deve separá-los com vírgula ( SHIFT + , ). Finalmente, você obterá o menor múltiplo comum clicando no botão igual.

Exercícios LCM resolvidos passo a passo

A seguir, mostraremos três exemplos de múltiplos mínimos comuns resolvidos passo a passo . Desta forma você poderá tentar resolver esses problemas e praticar um pouco do que explicamos neste artigo. É importante que você tente resolver os exercícios se quiser internalizar os conceitos, pois é necessário aplicar a teoria à realidade. Dito isto, deixamos você praticar com os exercícios:

Calcule o lcm de 4 e 6

Calcule o lcm de 6 e 9

Calcule o lcm de 30 e 40