Binômios - Matoridade

Nesta página você encontrará uma explicação do que é um binômio e, além disso, poderá ver exemplos de cada tipo de binômio. Além disso, mostramos as fórmulas usadas para resolver operações com binômios: multiplicação de binômios, binômio ao quadrado, binômio ao cubo,…

O que é um par?

Em álgebra, a definição de um binômio é:

Um binômio é um polinômio composto por apenas dois monômios . Em outras palavras, um binômio consiste em uma expressão algébrica com apenas 2 termos diferentes unidos pelo sinal de mais (+) ou pelo sinal de menos (-).

A palavra binomial vem do grego e é composta por dois componentes lexicais ( bi e nomos ), que significam o seguinte:

bi : prefixo que significa 2.
nomos : significa parte.

Podemos, portanto, deduzir o significado do binômio: polinômio com duas partes (ou 2 monômios).

Por outro lado, o conceito de par tem outro significado que não o matemático, nomeadamente que um par também pode designar um conjunto de duas personalidades que têm um papel protagonista na vida política, em determinadas modalidades desportivas ou mesmo no entretenimento. . Mas, obviamente, focaremos aqui na definição matemática do binômio.

Exemplos de binômios

Para finalizar a compreensão da noção de binômio, veremos vários exemplos desse tipo de polinômio:

Exemplo de um binômio quadrático:

$x^2+4x$

Exemplo de binômio de terceiro grau:

$x^3+5$

Exemplo de binômio de quarto grau:

$3x^4+8x^2$

Agora que sabemos o que é um binômio, veremos os diferentes tipos de binômios que existem e como as operações com binômios são resolvidas.

binômio ao quadrado

Um binômio quadrado é uma identidade notável, também chamada de produto notável ou igualdade notável. Resolver a potência de um binômio elevado a 2 depende se é um binômio de soma ou um binômio de diferença.

Uma soma binomial refere-se àquele binômio cujos dois termos são positivos, ou seja, uma soma binomial quadrada é:

$(a+b)^2$

Por outro lado, um binômio de diferença (ou subtração) é o conjugado do binômio de adição, ou seja, um de seus monômios tem sinal negativo. Portanto, a expressão algébrica para uma diferença binomial quadrada é:

$(a-b)^2$

Para calcular um binômio quadrado, é necessário aplicar uma fórmula que, como vimos, varia dependendo se se trata de uma adição ou subtração. Descubra como isso é feito nas fórmulas de igualdades notáveis , onde você pode ver todas as explicações passo a passo, bem como exemplos e exercícios resolvidos, e não apenas dessas 2 igualdades notáveis, mas de todas elas.

binômio ao cubo

Embora usados com menos frequência, os binômios cúbicos também são considerados produtos notáveis. Ou em outras palavras, existem regras matemáticas que permitem encontrar rapidamente o cubo de um binômio (você pode vê-las no link acima de fórmulas de identidades notáveis ).

Como antes, o resultado desta potenciação depende se é o cubo de uma soma:

$(a+b)^3$

Ou se, pelo contrário, a potência é constituída pelo cubo de uma diferença ou de uma subtração:

$(a-b)^3$

Logicamente, a principal diferença entre um binômio quadrado e um binômio cúbico é o expoente de potência. No entanto, a fórmula para um binômio ao cubo é muito mais complicada do que a de um binômio ao quadrado.

acordos notáveis

Existem, em particular, certos tipos de binômios que são um pouco particulares pelas suas características, pois correspondem a identidades notáveis (ou produtos notáveis) menos conhecidas.

Soma dos quadrados:
$a^2+b^2$
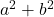
Diferença (ou subtração) de quadrados:
$a^2-b^2$
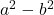
Soma dos cubos:
$a^3+b^3$
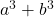
Diferença (ou subtração) de cubos:
$a^3-b^3$

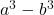
Ouro

$a$

$b$

são quaisquer dois monômios.

Embora essas expressões binomiais se pareçam muito com as que vimos acima (binomial ao quadrado e binomial ao cubo), se você olhar com atenção elas são diferentes. Nesse sentido, você também pode ver as fórmulas dos binômios notáveis e suas deduções clicando no link acima ⬆ fórmulas das identidades notáveis.⬆

multiplicação binomial

Uma das operações mais comuns com binômios é a multiplicação. A seguir veremos um exemplo de como calcular uma multiplicação entre binômios.

$(x^2+2x)\cdot (x-5)$

Para calcular a multiplicação binomial, devemos primeiro multiplicar cada termo do primeiro binômio por cada termo do segundo binômio:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

A seguir, agrupamos termos semelhantes, ou seja, possuem a mesma parte literal:

$\bm{x^3-3x^2 -10x}$

E assim conseguimos encontrar o resultado do produto entre os pares.

Produto de dois binômios com um termo comum

Quando os binômios que participam da multiplicação têm como termo comum a variável

$x,$

Existe uma fórmula para calcular rapidamente esta operação binomial:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Aqui mostramos um exercício resolvido para que você veja como aplicar esta fórmula:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

Binômio de Newton

O binômio de Newton , também chamado de teorema binomial, é uma fórmula usada para calcular as potências dos binômios.

A fórmula matemática para o binômio de Newton é a seguinte:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

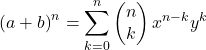
Ou equivalente:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Como você pode ver, esta fórmula é um pouco complexa de entender. É por isso que fizemos abaixo as potências dos binômios de menor grau para que você possa entender melhor:

fórmula para o teorema binomial de newton

Esta fórmula pode ser um pouco entediante para calcular binômios quadrados ou cúbicos, pois, como vimos acima, existem fórmulas mais simples. Porém, o binômio de Newton é muito útil para encontrar potências de grau superior, por exemplo, é amplamente utilizado para determinar um binômio elevado à quarta.

Mas para aplicar esta fórmula é necessário saber calcular um número combinatório, ou seja, a expressão algébrica do tipo

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, cálculo não é fácil. 🔍 É por isso que recomendamos que você pesquise como isso é feito em nosso mecanismo de busca no canto superior direito 🔎, você encontrará nosso artigo onde explicamos esta operação passo a passo.