O binômio de Newton é uma fórmula matemática usada para expressar a soma de dois termos elevados a uma determinada potência . Esta fórmula, em homenagem ao matemático britânico Isaac Newton, é usada em muitas áreas da matemática.
Por exemplo, tem utilidade em estatística, teoria das probabilidades e cálculo diferencial e integral. O teorema binomial nos permite calcular a potência de um binômio de forma simples.
Simplificando, o binômio de Newton é baseado em uma fórmula com a qual qualquer expressão algébrica da forma (a+b) n pode ser resolvida. Apesar de esta fórmula ter o nome de Isaac Newton, vale ressaltar que há controvérsias sobre sua origem.
Ou seja, algumas pesquisas sugerem encontrar a utilização do teorema binomial no Oriente Médio.
Quando o binômio de Newton foi desenvolvido?
O teorema binomial de Newton, também conhecido como binômio de Newton, foi desenvolvido em 1665 e comunicado pela primeira vez em duas cartas do oficial da Royal Society em 1676 .
Estas cartas foram uma resposta ao matemático alemão Gottfried Wilhelm von Leibniz, que procurava compreender melhor as investigações matemáticas em séries infinitas. Newton compartilhou os resultados de seu teorema e Leibniz reconheceu que era uma técnica útil para obter resultados em quadraturas ou séries.
Esta observação permitiu a Newton concluir que era possível operar sobre séries infinitas da mesma forma que sobre expressões polinomiais finitas . Embora Newton nunca tenha publicado seu teorema, o matemático britânico John Wallis publicou-o em sua Álgebra em 1685 e atribuiu sua criação a Newton.
Por que é chamado de binômio de Newton?
O binômio de Newton recebeu o nome do matemático e físico inglês Isaac Newton, que o desenvolveu no século XVII . Newton não foi o primeiro a descobrir este teorema, mas foi o primeiro a provar a sua validade para qualquer número inteiro positivo n.
O binômio de Newton é uma ferramenta matemática muito útil em álgebra e cálculo e é amplamente utilizado em áreas como física, estatística, engenharia e ciência da computação.
Qual é a fórmula binomial de Newton?
Como mencionamos anteriormente, o binômio de Newton é a fórmula pela qual as potências de um binômio podem ser encontradas . Para encontrar a referida potência binomial, são utilizados “coeficientes binomiais”. O termo anterior refere-se a sequências de combinações.
Com isso em mente, podemos decompor as fórmulas binomiais de Newton da seguinte forma:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
As expressões matemáticas que se referem ao desenvolvimento de (a+b) n são chamadas de entidades notáveis, e permitem obter uma fórmula geral que representa esta operação para qualquer número natural “n”.
Ao examinar os coeficientes de cada polinômio resultante, podemos notar uma sequência que segue o que é conhecido como Triângulo de Pascal .
A sequência do triângulo de Pascal começa com o número 1, e em cada linha subsequente os dígitos finais são sempre 1. Os valores intermediários são obtidos somando os dois números da linha anterior que estão diretamente acima do valor a ser calculado.
Como encontrar um termo no binômio de Newton?
Para encontrar um termo específico no binômio de Newton, a fórmula geral é usada:
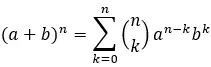
Ouro:
aeb são os coeficientes do binômio.
n é o expoente do binômio.
k é o termo específico que queremos encontrar.
Σ representa a soma de k=0 a n.
[nk] é o coeficiente binomial calculado pela seguinte fórmula:
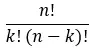
Portanto, a fórmula totalmente expandida é tal que:
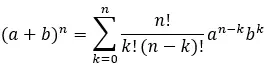
Exemplo de um binômio de Newton resolvido
Uma vez encontrados esses valores, eles são substituídos na fórmula e a expressão é resolvida para obter o termo específico. Por exemplo, se quiséssemos encontrar o quinto termo do binômio (2x + 3) 6 , teríamos:
um = 2x
b = 3
n=6
k = 5
Então, usando a fórmula:
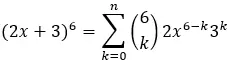
O quinto termo corresponde a k=5, portanto temos:
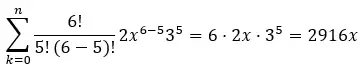
Portanto, o quinto termo do binômio (2x + 3) 6 é 2916x.
O que é um binômio de Newton de grau 5?
Um binômio de Newton de grau 5 é uma expressão algébrica da forma (a + b) 5 , onde “a” e “b” são variáveis e o expoente 5 indica o grau do binômio . Expandindo esta expressão, obtemos um polinômio quadrático que possui seis termos:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Cada termo deste polinômio é obtido combinando os coeficientes do binômio com as potências de “a” e “b”. Por exemplo, o segundo termo (5a 4 b) é obtido multiplicando o coeficiente binomial (5 escolha 1 = 5) por “a” elevado à quarta potência e por b elevado à primeira potência.
Os binômios de grau 5 de Newton são úteis em diferentes ramos da matemática e da física, como estatística, teoria das probabilidades e mecânica quântica.
Quais são as aplicações do binômio de Newton?
O binômio de Newton tem uma ampla variedade de aplicações em vários campos, incluindo:
- Cálculo de probabilidades : O teorema binomial é usado para calcular as probabilidades de eventos binomiais, como o lançamento de uma moeda ou o sucesso ou fracasso de uma série de testes.
- Teoria dos Números – O binômio de Newton é usado para expandir polinômios e simplificar equações na teoria dos números.
- Estatística : O binômio de Newton é usado para calcular distribuições binomiais e na construção de intervalos de confiança.
- Física – Na física, o teorema binomial é utilizado na teoria da relatividade e na mecânica quântica, entre outras áreas.
- Economia e Finanças : O binômio de Newton é usado para calcular o valor atual e futuro dos fluxos de caixa ao longo do tempo e na avaliação de opções financeiras.
- Programação e ciência da computação : o binômio de Newton é usado no desenvolvimento de algoritmos e programação de computadores.
Por que o binômio de Newton é importante?
O binômio de Newton é relevante porque é uma ferramenta matemática fundamental para o desenvolvimento da álgebra e da teoria dos números . Permite calcular o resultado da quadratura ou qualquer outra potência de um binômio, o que é muito útil para resolver equações e simplificar expressões algébricas.
Além disso, possui aplicações em áreas como estatística, probabilidade e física , entre outras. Em resumo, o binômio de Newton é um conceito essencial em matemática e compreendê-lo é crucial para o progresso em muitos campos de estudo.
Existem outras maneiras de expressar o binômio de Newton?
Sim, existem outras maneiras de expressar o binômio de Newton. Por exemplo, pode ser expresso em termos de coeficientes binomiais usando notação combinatória.
Além disso, pode ser expresso em termos de funções exponenciais e funções trigonométricas usando a fórmula de Euler. Da mesma forma, em termos de função gama usando a fórmula de Legendre. Estas expressões alternativas podem ser úteis em diferentes contextos e problemas matemáticos.
Exemplos binomiais de Newton
Vejamos então alguns exemplos simples de aplicação do binômio de Newton.
Exemplo 1: Calcule o termo de ordem 3 na expansão de (x + y) 5 .
Solução: Na expansão de (x + y) 5 , o coeficiente do primeiro termo é 1, o coeficiente do segundo termo é 5, o coeficiente do terceiro termo é 10, o coeficiente do quarto termo é 10, o o coeficiente do quinto termo é 5 e o coeficiente do sexto termo é 1.
O prazo da ordem 3 é, portanto:
10x 2 e 3
Exemplo 2: Encontre o termo independente na expansão de (2x – 1) 4 .
Solução: Na expansão de (2x – 1) 4 , o termo independente é encontrado na combinação (2x) p (-1) (4-p) , onde p é o valor que forma o expoente de (2x) p e (-1) (4-p) soma 4.
O termo independente é, portanto:
(2x) 2 (-1) 2 = 4
Exemplo 3: Encontre o termo de maior grau na expansão de (3x – 2y) 6 .
Solução: O termo de maior grau na expansão de (3x – 2y) 6 é encontrado na combinação (3x) p (-2y) (6-p) , onde p é o valor que forma o expoente de (3x) p e (-2y) (6-p) igual ao grau do binômio, que é 6.
Portanto, o termo de maior grau é:
(3x) 3 (-2y) 3 = -216x 3 e 3