Aqui você encontrará quais são as assíntotas verticais de uma função (com exemplos). Explicamos também como encontrar as assíntotas verticais de uma função e, além disso, você poderá praticar com exercícios resolvidos passo a passo.
O que é uma assíntota vertical?
Uma assíntota vertical de uma função é uma reta vertical cujo gráfico se aproxima indefinidamente sem nunca cruzá-la. Portanto, a equação para uma assíntota vertical é x=k , onde k é o valor da assíntota vertical.
Ou seja, k é uma assíntota vertical se o limite da função quando x se aproxima de k for infinito.
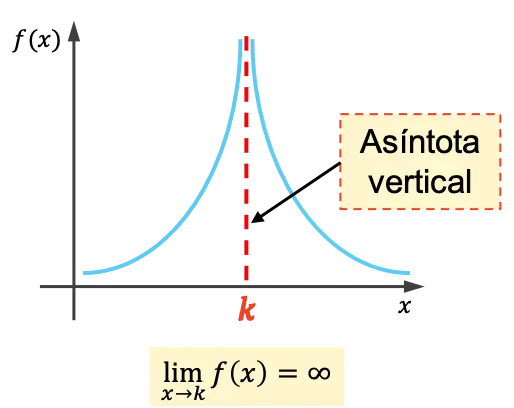
Como calcular a assíntota vertical de uma função
Para calcular a assíntota vertical de uma função, devem ser seguidos os seguintes passos:
- Encontre o domínio da função. Se todos os pontos estiverem no domínio, a função não possui assíntotas verticais.
- Calcule o limite da função em pontos que não estão no domínio.
- As assíntotas verticais da função serão todos os valores em que o limite dá infinito.
Observe que uma função pode ter mais de uma assíntota vertical. Por exemplo, o gráfico da função tangente tem infinitas assíntotas verticais.
➤ Veja: características da função tangente
Exemplo de assíntota vertical
Como exemplo, encontraremos todas as assíntotas da seguinte função racional para que você possa ver como isso é feito:
![]()
Em geral, os pontos onde existem assíntotas verticais não pertencem ao domínio da função. Portanto, primeiro calcularemos o domínio da função.
É uma função racional, então observamos quando o denominador desaparece para determinar os pontos que não pertencem ao domínio:
![]()
![]()
Portanto, o domínio da função são todos os números reais, exceto x=2:
![]()
Então x=2 poderia ser uma assíntota vertical da função. Para verificar isso, devemos calcular o limite da função neste ponto:
![]()
Neste caso obtivemos a indeterminação de um número entre zero e, portanto, para resolver o limite devemos calcular os limites laterais para saber se é mais infinito, menos infinito ou se o limite não existe. Porém, quando calculamos assíntotas verticais, não precisamos fazer os limites laterais, mas obter essa indeterminação é suficiente para dizer que se trata de uma assíntota vertical.
Resumindo, como o limite da função quando x tende a 2 dá infinito, x=2 é uma assíntota vertical.
Abaixo está a função representada graficamente. Como você pode ver, ela chega muito perto da reta x=2 (tanto da esquerda quanto da direita), mas nunca a cruza porque é uma assíntota vertical:

Além disso, podemos deduzir do gráfico os limites laterais da função no ponto x=2:
![]()
Problemas resolvidos de assíntotas verticais
Exercício 1
Calcule a assíntota vertical da seguinte função racional:
![]()
Não existe uma fórmula para calcular as assíntotas verticais de uma função, mas é preciso encontrar o domínio da função e ver em quais pontos onde a função não está definida o limite dá infinito.
Portanto, igualamos o denominador da função racional a 0 para encontrar os pontos que não pertencem ao domínio:
![]()
![]()
![]()
Assim, o domínio da função são todos os números reais, exceto x=1/2:
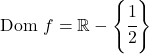
Então x=1/2 poderia ser uma assíntota vertical. Para verificar isso, calculamos o limite da função neste ponto:
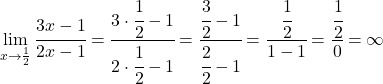
Então x=1/2 é uma assíntota vertical , já que o limite da função neste ponto dá infinito.
Exercício 2
Encontre todas as assíntotas verticais da seguinte função fracionária:
![]()
Primeiro, igualamos o denominador da fração a zero para ver quais valores não estão no domínio da função:
![]()
Resolvemos a equação quadrática incompleta:
![]()
![]()
O domínio da função racional é, portanto:
![]()
Então, para determinar quais desses dois valores são assíntotas verticais, resolvemos o limite da função em cada ponto:
![]()
![]()
Os dois limites dão infinito, então x=3 e x=-3 são as duas assíntotas verticais da função do problema .
Exercício 3
Encontre, se tiver, todas as assíntotas verticais da seguinte função racional:
![]()
➤ Veja: zero entre zero indeterminação
Primeiro, resolvemos a equação do denominador quadrático para encontrar os valores que anulam o denominador da fração:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Portanto o domínio da função é:
![]()
Então, primeiro calculamos o limite da função em x=1:
![]()
E, por outro lado, resolvemos o limite da função quando x tende para -3:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
O limite anterior dá a forma indeterminada zero entre zero, então para resolvê-lo precisamos fatorar os polinômios. Caso você tenha alguma dúvida sobre como resolvemos o limite, você pode ver a explicação completa de como resolver esse tipo de indeterminação no link do demonstrativo do exercício.
Neste caso, apenas o limite da função no ponto x=1 dá infinito, então x=1 é a única assíntota vertical da função .