▷ Assíntota oblíqua de uma função (exercícios resolvidos)

Neste artigo explicamos o que são as assíntotas oblíquas de uma função. Você aprenderá quando uma função tem uma assíntota oblíqua e como ela é calculada. E, além disso, você poderá ver exemplos de assíntotas oblíquas e praticar com exercícios resolvidos passo a passo.

O que é uma assíntota oblíqua?

A assíntota oblíqua de uma função é uma reta inclinada da qual seu gráfico se aproxima indefinidamente, sem nunca cruzá-la. Consequentemente, todas as assíntotas oblíquas são retas com a equação y=mx+n .

A inclinação e a origem de uma assíntota oblíqua são calculadas usando as seguintes fórmulas:

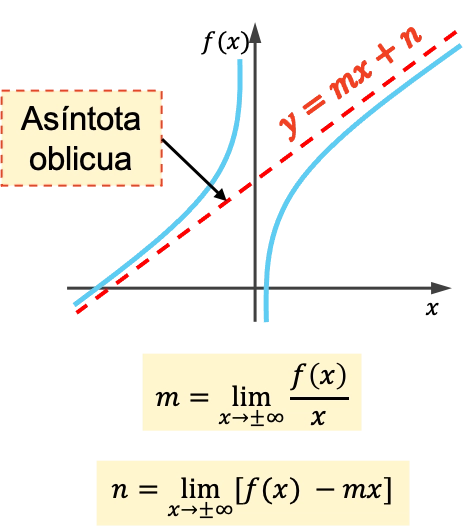
Como calcular a assíntota oblíqua de uma função

Para calcular a assíntota oblíqua de uma função, devem ser executados os seguintes passos:

Calcule o limite ao infinito da função dividida por x.
Se o limite acima resultar em um número real diferente de zero, significa que a função tem uma assíntota oblíqua. E mais, a inclinação da referida assíntota oblíqua será o valor obtido no limite.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

Neste caso, resta calcular a interceptação da assíntota oblíqua resolvendo o seguinte limite:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Nota: os limites devem ser calculados em mais e menos infinito, mas normalmente dão o mesmo resultado e por isso simplificamos colocando ±∞. Mas se os limites em mais e menos infinito fossem diferentes, a assíntota oblíqua esquerda e a assíntota oblíqua direita teriam de ser calculadas separadamente.

Exemplo de assíntota oblíqua

A seguir, pegaremos a assíntota oblíqua da seguinte função racional para que você possa ver um exemplo de como isso é feito:

$f(x)=\cfrac{x^2+1}{x}$

As assíntotas oblíquas são do tipo

$y=mx+n.$

Então, primeiro calculamos a inclinação da reta

$m$

com sua fórmula correspondente:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

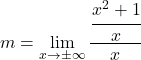
Para resolver este limite devemos aplicar as propriedades das frações:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

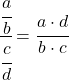
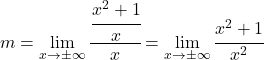
E agora calculamos o limite:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

Nesse caso, o resultado da indeterminação do infinito entre o infinito é a divisão dos coeficientes de x de maior grau, pois o numerador e o denominador são da mesma ordem.

O limite acima fornece um número real diferente de zero, então a função tem uma assíntota oblíqua. Vamos agora calcular a interceptação y

$n$

da assíntota usando sua fórmula correspondente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

Tentamos calcular o limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Mas obtemos indeterminação infinito menos infinito. É, portanto, necessário reduzir os termos a um denominador comum. Para fazer isso, multiplicamos e dividimos x pelo denominador da fração:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Agora que os dois termos têm o mesmo denominador, podemos agrupá-los:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

Operamos no numerador:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

E finalmente, resolvemos o limite:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Então n =0. Portanto, a assíntota oblíqua é uma função linear:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

A função estudada está representada no gráfico abaixo. Como você pode ver, a função chega muito perto da reta y=x mas nunca a toca porque é uma assíntota oblíqua:

Exercícios resolvidos sobre assíntotas oblíquas

Exercício 1

Encontre a assíntota oblíqua da seguinte função racional:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Veja a solução

As assíntotas oblíquas têm a forma

$y=mx+n$

, é portanto necessário calcular os parâmetros m e n . Primeiro calculamos m aplicando sua fórmula:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

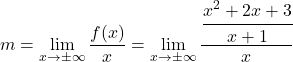
Simplificamos a fração aplicando as propriedades das frações:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

E resolvemos o limite:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Então m = 1. Vamos agora calcular a interceptação da assíntota oblíqua aplicando sua fórmula:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

Tentamos calcular o limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Mas obtemos a forma indeterminada infinito menos infinito. Devemos, portanto, reduzir os termos a um denominador comum e depois agrupá-los:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

E finalmente, resolvemos o limite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

Resumindo, a assíntota oblíqua da função é:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Exercício 2

Encontre todas as assíntotas oblíquas da seguinte função racional:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Veja a solução

Primeiro, usamos a fórmula para a inclinação da assíntota oblíqua:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

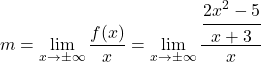
Simplificamos a fração aplicando as propriedades das frações:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

E determinamos o limite:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

O limite fornece um número real diferente de zero, portanto é uma função racional com uma assíntota oblíqua cuja inclinação é 2.

Agora vamos calcular a interceptação aplicando a fórmula correspondente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

Tentamos calcular o limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Mas obtemos a diferença indeterminada dos infinitos. Portanto, reduzimos os termos a um denominador comum e então operamos:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

E finalmente, resolvemos o limite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

Em resumo, a assíntota oblíqua da função fracionária é:

$y = mx+n$

$\bm{y=2x-6}$

O que é uma assíntota oblíqua?

Como calcular a assíntota oblíqua de uma função

Exemplo de assíntota oblíqua

Exercícios resolvidos sobre assíntotas oblíquas

Exercício 1

Exercício 2

Deixe um comentário Cancelar resposta