Assíntota horizontal

Neste artigo explicamos o que são as assíntotas horizontais de uma função e como são calculadas. Além disso, você encontrará vários exemplos deste tipo de assíntotas para compreender totalmente o conceito e, além disso, poderá praticar com exercícios resolvidos de assíntotas horizontais.

O que é uma assíntota horizontal?

Uma assíntota horizontal de uma função é uma linha horizontal da qual seu gráfico se aproxima indefinidamente sem nunca cruzá-la. Portanto, a equação para uma assíntota horizontal é y=k , onde k é o valor da assíntota horizontal.

Ou seja, k é uma assíntota horizontal se o limite da função quando x se aproxima do infinito for igual a k .

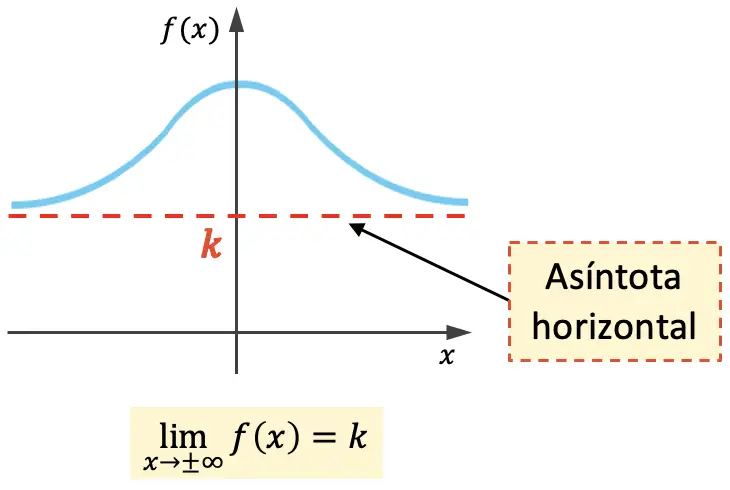
assíntota horizontal de uma função

A função acima possui uma assíntota horizontal em ambos os lados do gráfico, mas uma função só pode ter uma assíntota horizontal em um lado:

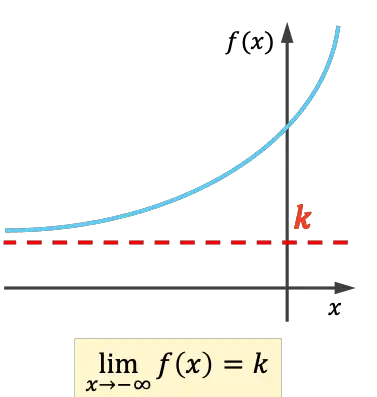
  • A função tem uma assíntota horizontal à esquerda se o limite pelo menos ao infinito fornecer um número real.
  • A função tem uma assíntota horizontal à direita se o limite mais infinito fornecer um número real.
assíntota horizontal de uma função da esquerda
assíntota horizontal à direita

Como calcular a assíntota horizontal de uma função

Para calcular a assíntota horizontal de uma função, devem ser seguidos os seguintes passos:

  1. Calcule o limite da função ao infinito (+∞ e -∞).
  2. Se um limite ao infinito dá um número real (k), a reta y=k é uma assíntota horizontal da função.
  3. Se nenhum dos limites corresponder a um número real, a função não possui assíntotas horizontais.

Exemplo de assíntota horizontal

Para que você possa ver um exemplo de como isso é feito, removeremos todas as assíntotas horizontais da seguinte função racional:

f(x)=\cfrac{x+1}{x-1}

Para determinar as assíntotas horizontais, é necessário calcular o limite em menos infinito e em mais infinito da função:

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Veja: como resolver a indeterminação infinita entre infinitos

Os dois limites no infinito dão 1, então y=1 é a única assíntota horizontal da função.

Abaixo está a função representada graficamente. Como você pode ver, a função chega muito perto de y=1 (tanto em mais infinito quanto em menos infinito), mas nunca a toca porque é uma assíntota horizontal.

exemplo de assíntota horizontal

Nota: em alguns casos especiais, a função intercepta a assíntota horizontal em um ou mais pontos, mas em geral o gráfico de uma função nunca cruza as suas assíntotas.

Por outro lado, esta função também possui uma assíntota vertical em x=1. Porque, como você pode ver no gráfico, ele chega muito perto da reta x=1, mas nunca atinge esse valor.

Problemas resolvidos de assíntotas horizontais

Exercício 1

Encontre a assíntota horizontal, se houver, da seguinte função fracionária:

\displaystyle f(x)= \frac{4x+3}{2x-1}

Para determinar as assíntotas horizontais da função racional, é necessário calcular os limites no infinito da função:

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

Neste caso, o resultado da forma indeterminada ∞/∞ é a divisão dos coeficientes do x de maior grau, pois o numerador e o denominador são da mesma ordem.

Os limites em mais infinito e menos infinito da função dão 2, então y=2 é uma assíntota horizontal e é a única que a função possui.

Exercício 2

Encontre todas as assíntotas horizontais da seguinte função racional com raiz:

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Para encontrar as assíntotas horizontais da função, primeiro calculamos o limite no infinito positivo:

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

E então resolvemos o limite da função até menos infinito:

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Se você tiver alguma dúvida sobre como foram resolvidos os limites ao infinito, recomendamos conferir no link acima como resolver a indeterminação infinita entre o infinito.

Neste caso, obtivemos dois valores diferentes dos limites no infinito. A função, portanto, tem duas assíntotas horizontais: y=3 é uma assíntota horizontal da função à direita e, por outro lado, y=-3 é uma assíntota horizontal da função à esquerda.

Exercício 3

Calcule as assíntotas horizontais da seguinte função definida por partes:

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Para calcular as assíntotas horizontais da função, não existe fórmula, mas é necessário calcular os limites para mais e menos infinito.

Assim, para encontrar o limite pelo menos infinito, tomamos a função definida na primeira seção:

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Assim, a linha y=0 é uma assíntota horizontal à esquerda da função.

E agora calculamos o limite em mais infinito tomando a função definida na segunda seção:

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

Assim, a reta y=1/2 é uma assíntota horizontal à direita da função.

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima