Ângulo entre uma reta e um plano

Aqui você descobrirá como o ângulo entre uma linha e um plano é calculado. Você também poderá ver exemplos e, além disso, praticar com exercícios resolvidos passo a passo de ângulos entre retas e planos.

Qual é o ângulo entre uma linha e um plano?

O ângulo entre uma linha e um plano é o ângulo entre a linha e sua projeção ortogonal no plano.

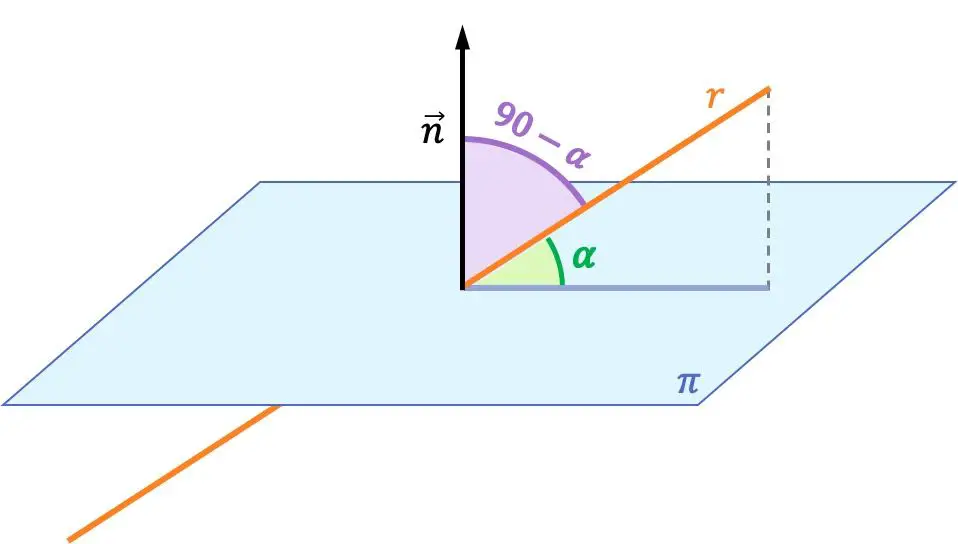
O ângulo entre uma reta e um plano é o complemento do ângulo entre essa reta e o vetor normal ao plano. Portanto, o ângulo entre uma reta e um plano é calculado a partir do ângulo entre o vetor direção da reta e o vetor normal do plano.

Fórmula do ângulo entre uma reta e um plano

Para deduzir a fórmula do ângulo entre um plano e uma reta, você precisa saber como encontrar o ângulo entre dois vetores . Na página do link você encontrará a explicação, bem como exemplos e exercícios resolvidos passo a passo, então se não lembra como fazer, recomendamos que dê uma olhada.

Assim, como o ângulo entre uma reta e um plano é complementar ao ângulo entre o vetor diretor da dita reta

$(\vv{\text{v}}_r)$

e o vetor normal ao referido plano

$(\vv{n})$

, da fórmula do ângulo entre dois vetores deduzimos que o ângulo entre uma reta e um plano é equivalente à seguinte expressão:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Portanto, a fórmula para o ângulo entre uma linha e um plano é :

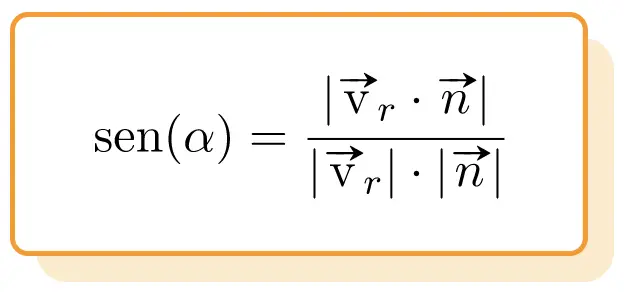
ângulo entre uma linha e um plano de fórmula

Ouro:

$\vv{\text{v}}_r$

é o vetor direto da linha.
$\vv{n}$

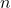
é o vetor normal ao plano.

Exemplo de cálculo do ângulo entre uma linha e um plano

Para que você veja como resolver esse tipo de problema, aqui está um exemplo de cálculo do ângulo entre uma reta e um plano:

Calcule o ângulo formado pela reta
$r$

com o avião

$\pi.$

Sejam suas equações:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

A reta é expressa na forma de equações paramétricas, então seu vetor direção é:

$\vv{\text{v}}_r = (-1,4,-3)$

Por outro lado, o plano é definido na forma de uma equação implícita (ou geral), portanto seu vetor normal é:

$\vv{n} = (1,-1,4)$

Assim, uma vez conhecido o vetor diretor da reta e o vetor normal do plano, aplicamos a fórmula do ângulo entre uma reta e um plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Substituímos os vetores na fórmula:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

E fazemos os cálculos:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Finalmente, invertemos o seno com a calculadora e encontramos o valor do ângulo:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

O ângulo entre a linha e o plano é, portanto, de aproximadamente 51,80º.

Devemos levar em conta que se alguma vez obtivermos um resultado de 0º, isso significa que a reta e o plano são paralelos ou que a reta está contida no plano. E se o ângulo for igual a 90º, implica que a reta e o plano são perpendiculares.

Problemas resolvidos do ângulo entre uma linha e um plano

Exercício 1

Encontre o ângulo formado pela linha

$r$

com o avião

$\pi.$

Sejam suas equações:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

veja solução

A reta é expressa como uma equação contínua, então seu vetor direção é:

$\vv{\text{v}}_r = (2,-1,-3)$

Por outro lado, o plano está na forma de uma equação implícita (ou geral), então seu vetor normal é:

$\vv{n} = (3,1,2)$

Assim, uma vez conhecido o vetor diretor da reta e o vetor normal do plano, usamos a fórmula para o ângulo entre uma reta e um plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Finalmente, invertemos o seno e encontramos o valor do ângulo:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Portanto, o ângulo entre a reta e o plano é 4,10º.

Exercício 2

Determine o ângulo formado pela linha

$r$

com o avião

$\pi.$

Sejam suas equações:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

veja solução

A reta é expressa com suas equações implícitas (ou gerais), portanto é necessário encontrar o vetor diretor da reta calculando o produto vetorial dos vetores normais aos 2 planos que determinam a reta:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

Por outro lado, o vetor normal ao plano é:

$\vv{n} = (-4,2,0)$

Assim, uma vez conhecido o vetor diretor da reta e o vetor normal do plano, usamos a fórmula para o ângulo entre uma reta e um plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Finalmente, invertemos o seno e encontramos o valor do ângulo:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Portanto, o ângulo entre a reta e o plano é 46,33º.

Exercício 3

Encontre, usando a fórmula do ângulo entre uma reta e um plano, o valor de

$k$

necessário para o direito

$r$

e o avião

$\pi$

ser paralelo.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

veja solução

Primeiro, a reta é expressa como uma equação vetorial, então seu vetor direção é:

$\vv{\text{v}}_r = (4,-1,3)$

Por outro lado, o plano tem a forma de uma equação geral, então seu vetor normal é:

$\vv{n} = (4,3,k)$

Assim, para que os dois elementos geométricos sejam paralelos, o ângulo entre eles deve ser zero. Portanto, a fórmula para o ângulo entre uma linha e um plano é:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Assim, o produto escalar entre o vetor de direção da reta e o vetor normal deve ser zero. E a partir desta equação podemos determinar o valor da incógnita

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Finalmente, se você achou este artigo útil, provavelmente também está interessado em como encontrar o ângulo entre dois planos . Na página de links você encontrará uma explicação bem detalhada bem como a fórmula necessária para calcular o ângulo entre dois planos diferentes e, além disso, poderá ver exemplos e exercícios resolvidos passo a passo para poder praticar e entender como isso é feito perfeitamente.

Qual é o ângulo entre uma linha e um plano?

Fórmula do ângulo entre uma reta e um plano

Exemplo de cálculo do ângulo entre uma linha e um plano

Problemas resolvidos do ângulo entre uma linha e um plano

Exercício 1

Exercício 2

Exercício 3

Deixe um comentário Cancelar resposta