Ângulo entre duas linhas (fórmula)

Nesta página você encontrará a explicação de como calcular o ângulo entre duas retas (fórmula). Você também poderá ver diversos exemplos e, além disso, poderá praticar com exercícios resolvidos passo a passo.

Qual é o ângulo entre duas linhas?

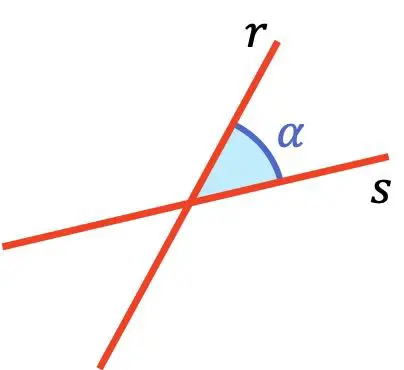
O ângulo entre duas linhas é o menor ângulo entre essas duas linhas.

No plano existem quatro tipos de retas dependendo do ângulo que formam entre elas: retas que se cruzam (entre 0º e 90º), retas perpendiculares (90º), retas paralelas (0º) e retas coincidentes (0º).

linhas que se cruzam

As linhas que se cruzam se cruzam em um ângulo agudo entre 0º e 90º.

Linhas retas perpendiculares

ângulo entre duas linhas perpendiculares

As linhas perpendiculares se cruzam em um ângulo reto de 90º.

Linhas paralelas

As linhas paralelas nunca se tocam e formam um ângulo de 0º entre elas.

linhas coincidentes

Duas retas coincidentes possuem todos os pontos em comum e, portanto, existe sempre um ângulo de 0º entre elas.

Concluindo, o cálculo do ângulo entre duas retas paralelas, coincidentes ou perpendiculares é imediato: as retas paralelas e as retas coincidentes formam um ângulo de 0 graus, pois têm a mesma direção, e as retas perpendiculares se cruzam com um ângulo de 90 graus . Por outro lado, para encontrar o ângulo entre duas retas que se cruzam, deve-se aplicar uma fórmula (veremos a seguir).

Como é calculado o ângulo entre duas linhas?

Existem duas maneiras de calcular o ângulo entre duas linhas. O primeiro método utiliza o vetor de direção de cada reta e o segundo método é baseado na inclinação de cada reta.

Nenhum procedimento é melhor que o outro, na verdade ambos são bastante fáceis, mas dependendo de como as linhas são expressas, um método ou outro é prático. Portanto, recomendamos que você saiba usar ambos os métodos matemáticos.

Método de orientação vetorial de linha

A fórmula para calcular o ângulo entre duas linhas usando seus vetores de direção é:

Dados os vetores de direção de duas linhas diferentes:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

O ângulo entre essas duas linhas pode ser calculado com a seguinte fórmula:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Ouro

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

são os módulos dos vetores

$\vv{\text{u}}$

$\vv{\text{v}}$

respectivamente.

Lembre-se de que a fórmula para a magnitude de um vetor é:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Vamos ver como encontrar o ângulo entre duas linhas com um exemplo:

Calcule o ângulo entre as duas linhas a seguir:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Para calcular o ângulo entre as duas retas, primeiro você deve encontrar o vetor de direção de cada reta.

o certo

$r$

é expresso na forma de uma equação paramétrica , portanto os componentes do vetor que marca sua direção são:

$\vv{r} = (-3,4)$

e a lei

$\displaystyle s$

é definido na forma de uma equação implícita (ou geral), então as coordenadas de seu vetor de direção são:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Agora que sabemos o vetor diretor de cada reta, podemos usar a fórmula do ângulo entre duas retas:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Portanto, determinamos a magnitude dos dois vetores:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Realizamos as operações vetoriais da fórmula do ângulo:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

E, por fim, calculamos o ângulo formado pelas duas retas com o inverso do cosseno:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Lembre-se que você pode calcular o inverso do cosseno usando a calculadora com a tecla

$\boxed{\cos ^{-1}}.$

método de inclinação

Obviamente, para entender esse método, você precisa conhecer a inclinação da reta . Você pode revisar este conceito no link, onde encontrará uma explicação detalhada do que significa, como é calculado, exemplos e exercícios resolvidos da inclinação de uma reta.

A fórmula para calcular o ângulo entre duas linhas a partir de suas inclinações é:

Ou duas linhas distintas:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

O ângulo entre essas duas linhas pode ser determinado com a seguinte fórmula:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Ouro

$m_1$

$m_2$

são as inclinações das linhas

$r_1$

$r_2$

respectivamente.

Vamos ver como calcular o ângulo entre duas retas usando suas inclinações com um exemplo:

Encontre o ângulo entre as duas linhas a seguir:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

A inclinação de cada linha é o número antes da variável

$x:$

$m_r = 4$

$m_s = -3$

Portanto, o ângulo entre as duas linhas pode ser encontrado aplicando a fórmula da inclinação:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

E finalmente encontramos o ângulo com o inverso da tangente:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Lembre-se que você pode calcular o inverso da tangente usando a calculadora com a tecla

$\boxed{\tan ^{-1}}.$

Acabamos de ver um exemplo com os declives de duas retas expressos como uma equação explícita, mas se estivessem na forma de uma equação de declive de ponto, este mesmo procedimento teria que ser utilizado.

Resolvendo problemas de ângulo entre duas linhas

Exercício 1

Determine o ângulo formado pelas duas retas a seguir:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

veja solução

Neste caso, usaremos o método do vetor de direção. Portanto, devemos primeiro encontrar o vetor diretor de cada reta. Ambas as retas são expressas como equações paramétricas, portanto os componentes de seus vetores de direção são os termos na frente do parâmetro

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Agora que sabemos o vetor diretor de cada reta, podemos usar a fórmula do ângulo entre duas retas:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Portanto, determinamos a magnitude dos dois vetores:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Resolvemos o produto escalar entre os dois vetores do numerador e a multiplicação dos módulos do denominador:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

E, por fim, encontramos o ângulo formado pelas duas retas fazendo o inverso do cosseno:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Exercício 2

Encontre o ângulo entre as duas linhas a seguir:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

veja solução

Resolveremos este problema usando o método do vetor de direção, então primeiro precisamos encontrar o vetor de direção de cada reta. o certo

$r$

é expresso na forma de uma equação geral (ou implícita), tal que os componentes do vetor que marca sua direção são:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

e a lei

$\displaystyle s$

é definido na forma de uma equação contínua, então as coordenadas cartesianas de seu vetor de direção são os números dos denominadores:

$\vv{s} = (6,3)$

Uma vez conhecido o vetor diretor de cada reta, podemos usar a fórmula para o ângulo entre duas retas:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Portanto, determinamos os módulos dos dois vetores:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Realizamos as operações entre vetores da fórmula do ângulo:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

E, por fim, calculamos o ângulo formado pelas duas retas com o inverso do cosseno:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Exercício 3

Qual é o ângulo entre as duas linhas a seguir?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

veja solução

Neste caso, utilizaremos o método das inclinações das retas para descobrir o ângulo que elas formam, já que as retas estão na forma de uma equação explícita.

A inclinação de cada linha é o número que acompanha a variável independente

$x:$

$m_r = -2$

$m_s = 5$

Portanto, o ângulo entre as duas linhas pode ser determinado aplicando a fórmula da inclinação:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

E finalmente encontramos o ângulo entre as duas retas invertendo a tangente:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Exercício 4

Encontre a equação da reta que passa pelo ponto

$P(5,-1)$

e faz um ângulo de 45º com a linha

$r.$

Seja dita linha:

$\displaystyle r: \ y=2x+4$

veja solução

Para resolver o problema, ligaremos

$s$

à direita que vamos calcular. Além disso, usaremos o método da inclinação porque conhecemos a inclinação da reta

$r:$

$m_r=2$

A partir da fórmula do ângulo entre duas retas (método da inclinação) podemos obter o valor da inclinação da reta

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Substituímos os valores conhecidos na fórmula:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

E tentamos resolver a equação resultante:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

O valor absoluto da equação dificulta um pouco a solução, pois é necessário analisar tanto as opções positivas quanto as negativas:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Temos, portanto, duas soluções possíveis: uma reta com inclinação -3 e outra reta com inclinação um terço.

A fórmula para a equação ponto-inclinação de uma reta é:

$y-y_0=m(x-x_0)$

Portanto, uma vez conhecida a inclinação das duas retas possíveis, podemos escrever a equação ponto-inclinação de cada reta com o ponto pelo qual elas devem passar de acordo com a afirmação,

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Qual é o ângulo entre duas linhas?

Como é calculado o ângulo entre duas linhas?

Método de orientação vetorial de linha

método de inclinação

Resolvendo problemas de ângulo entre duas linhas

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta