Como calcular adição e subtração de matrizes

Nesta página veremos como adicionar e subtrair matrizes . Você também tem exemplos que o ajudarão a entendê-lo perfeitamente e exercícios resolvidos para que você possa praticar. Você também encontrará todas as propriedades de adição de matrizes.

Como adicionar e subtrair matrizes?

Para calcular uma adição (ou subtração) de duas matrizes, deve-se somar (ou subtrair) os elementos que ocupam a mesma posição nas matrizes.

Exemplos:

exemplos de adição e subtração de matrizes 2x2, operações com matrizes

Observe que para adicionar ou subtrair duas matrizes, elas devem ter a mesma dimensão. Por exemplo, as seguintes matrizes não podem ser adicionadas porque a primeira é uma matriz 2×2 e a segunda é uma matriz 3×2:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

Exercícios resolvidos para adição e subtração de matrizes

Exercício 1

Calcule a seguinte soma de matrizes 2×2:

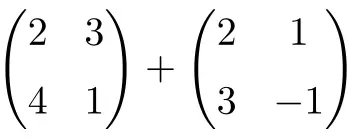
exercício resolvido passo a passo para adição de matrizes 2x2

É uma soma de duas matrizes quadradas de dimensão 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

Exercício 2

Execute a seguinte subtração de matriz:

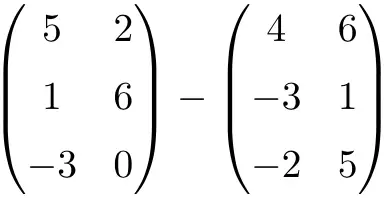
exercício resolvido subtração passo a passo de matrizes, operações com matrizes

É uma subtração de duas matrizes de dimensão 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

Exercício 3

Encontre o resultado da seguinte soma de matrizes de dimensão 3×3:

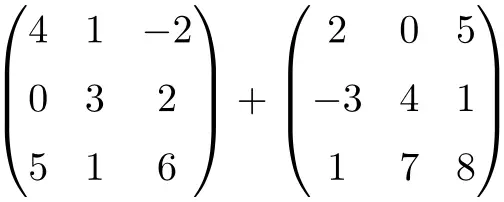
exercício resolvido passo a passo de adição de matrizes 3x3, operações com matrizes

É uma soma de duas matrizes quadradas de ordem 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

Exercício 4

Calcule a seguinte adição e subtração de matrizes quadradas de ordem 2:

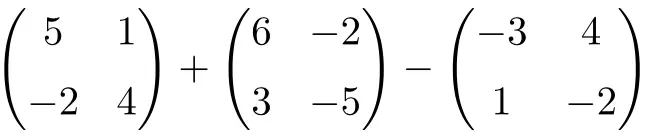
exercício resolvido passo a passo adição e subtração de matrizes 2x2, operações com matrizes

É uma operação combinada com adição e subtração de matrizes quadradas de ordem 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Então, primeiro adicionamos as matrizes à esquerda:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

E então calculamos a subtração de matrizes:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

Exercício 5

Resolva a seguinte adição e subtração de matrizes:

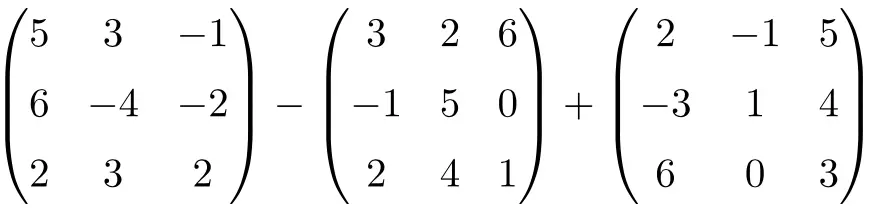
exercício resolvido passo a passo adição e subtração de matrizes 3x3, operações com matrizes

É uma operação combinada de subtração e adição de matrizes quadradas de ordem 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Primeiro, resolvemos a subtração de matrizes:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

E finalmente adicionamos as matrizes:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

Agora que você sabe como somar e subtrair matrizes, é um bom momento para ver como multiplicar matrizes , certamente a mais importante das operações com matrizes. Você também encontrará exercícios passo a passo de multiplicação de matrizes resolvidos para praticar, como em todas as páginas deste site. 😉

Adicionar propriedades de matriz

A adição de matrizes tem as seguintes características:

  • A adição de matrizes tem a propriedade comutativa :

\displaystyle A +B = B + A

Portanto, a ordem em que somamos as matrizes é a mesma. Para demonstrar isso, adicionaremos duas matrizes alterando sua ordem e você verá como o resultado é o mesmo.

Portanto, procedemos à adição de duas matrizes em uma determinada ordem:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

Observe que se invertermos a ordem de adição das matrizes, o resultado permanece o mesmo:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

  • Outra propriedade da adição de matrizes é a do elemento oposto:

\displaystyle A + (-A) =0

Em outras palavras, se somarmos uma matriz mais a mesma matriz, mas com todos os seus elementos com sinais alterados, o resultado será uma matriz zero:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

  • A adição de matrizes também possui a propriedade do elemento neutro:

\displaystyle A + 0 =A

Esta propriedade é a mais óbvia, refere-se ao fato de que qualquer matriz mais uma matriz cheia de zeros equivale à mesma matriz:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

  • A adição de matrizes tem a propriedade associativa:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

Portanto, a ordem em que somamos as matrizes é a mesma. Veja o exemplo a seguir, onde somamos 3 matrizes com ordens diferentes e o resultado é o mesmo:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima