O que é fatoração polinomial? É uma técnica matemática que permite decompor um polinômio em fatores ou expressões mais simples. E graças a esta simplificação poderemos realizar operações entre diversas expressões algébricas de forma mais fácil e confortável. Assim, ao longo deste artigo, discutiremos diferentes métodos de fatoração de polinômios e todos os casos possíveis de fatoração.
Como fatorar um polinômio?
Existem muitos métodos de fatoração que possuem sua própria estrutura de solução, mas, em última análise, dependem da mesma coisa. Além disso, você também pode encontrar uma grande variedade de casos relacionados à configuração polinomial. É por isso que nas seções a seguir discutiremos todos os procedimentos existentes e quando usar cada um deles. Por fim, iremos aplicá-lo a um exemplo real para que você termine de adquirir os conceitos.
Fatore um polinômio com a regra de Ruffini
O método mais utilizado para fatorar polinômios é a regra de Ruffini , pois é fácil de usar e o resultado pode ser encontrado rapidamente. O normal é usar esta técnica para fatorar polinômios de grau maior que dois, ou mesmo às vezes para fatorar polinômios de segundo grau. Uma vez que permite obter as raízes deste polinômio de forma muito gráfica. Embora esse uso seja explicado na próxima seção, que enfoca as raízes de uma expressão matemática desse tipo.
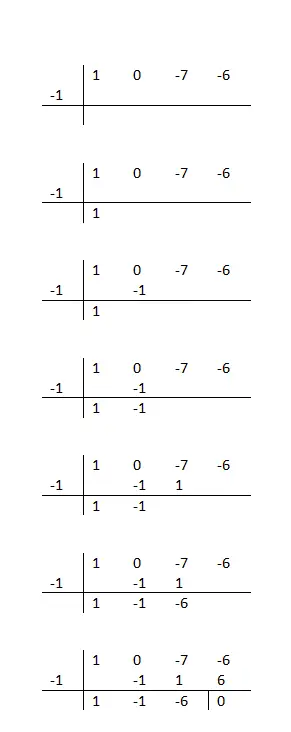
Como fazer Ruffini para fatorar polinômios?
Basicamente teremos que escrever os coeficientes do dividendo em uma linha horizontal e o valor de uma possível raiz do polinômio ao lado. Dizemos possível porque teremos que procurar um divisor que nos permita obter um resto igual a zero. Caso contrário, este número não será uma raiz válida e você terá que continuar tentando.
Como dica, recomendamos que você experimente apenas os números divisores do termo independente (último valor da linha horizontal). Então, para saber se o número que você escolheu está correto, basta seguir a seguinte sequência de cálculos :
Você diminui o coeficiente, multiplica-o pela raiz que está testando, escreve abaixo do próximo coeficiente e faz a adição vertical. Basta repetir estes passos até o final e, quando terminar, você saberá se este valor está correto ou não. Uma vez que apenas os números que dão um resto zero serão válidos.
Se o procedimento matemático que você precisa seguir não estiver muito claro para você, veja o exemplo na coluna à esquerda deste texto. Além disso, recomendamos tentar fatorar o seguinte polinômio: x³ + 2x² – x – 2 (com base no exemplo). E por último, para saber se resolveu o exercício corretamente ou não, você pode comparar seu resultado com este:
- Expressão em excesso = x² + 3x + 2
- resto = 0
Faremos agora uma breve explicação sobre a aplicação de Ruffini na fatoração . Porém, se você quiser saber detalhadamente como esse recurso matemático é utilizado, recomendamos que você acesse o último artigo que vinculamos, pois lá está tudo muito bem explicado. Dito isto, vamos começar explicando como fatorar polinômios com a regra de Ruffini:
- Desenhamos a grade: como podemos ver na imagem acima, criaremos uma caixa na qual faremos o Ruffini. Basicamente, deve-se escrever os coeficientes da expressão ordenados horizontalmente e sem deixar aqueles que têm valor zero. No final, você deverá ter uma representação semelhante à da imagem mas com os valores do seu polinômio.
- Calculamos as raízes: depois de desenharmos a estrutura e nos certificarmos de que todos os números estão escritos corretamente, procederemos ao cálculo da raiz. Você precisará encontrar as raízes seguindo a sequência de cálculo de que falamos logo acima desta lista (com as imagens).
- Expressamos a raiz na forma (x – a): quando temos todas as raízes do polinômio então devemos expressá-las na seguinte forma (x – a). Levando em consideração que a são os valores que obtivemos, por exemplo se extraímos como resultado x = 2, x = -2 e x = 4, então obteremos (x – 2), (x + 2) e ( x – 4).
- Reunimos todos os fatores em uma única expressão: finalmente, quando já tivermos todas as raízes expressas no formato correto, teremos apenas que reuni-las em uma única expressão algébrica. Continuando com o exemplo anterior, teríamos algo assim: (x – 2) · (x + 2) · (x – 4).
Fatore um polinômio usando as raízes de um polinômio
Explicamos parcialmente o conceito de raiz de um polinômio na seção de Ruffini. Mas, a definição exata seria: a raiz de um polinômio P(x) é um valor numérico a, tal que P(a) = 0 . É portanto um número capaz de anular a função ou polinômio em questão. Em resumo, poderíamos dizer que serve para decompor um polinômio em um produto de fatores.
Por exemplo, se recebermos a seguinte expressão x² − x − 2 e a fatorarmos usando a regra de Ruffini ou simplesmente resolvendo a equação quadrática x² − x − 2 = 0. Obteremos dois valores de x = -1 e x = 2, então se os mudarmos para o formato (x – a) e os juntarmos, chegaremos à seguinte expressão: (x + 1) (x − 2), ou seja, o polinômio fatorado . E podemos aplicar isto a polinómios de grau maior que dois, embora a expressão seja composta por mais de um termo.
Fatoração de um polinômio por extração de fator comum
Quando queremos fatorar polinômios sem termo independente ou expressões que possuem um fator comum em todos os termos, podemos simplificar o polinômio usando esta técnica. Basicamente envolve aplicar a propriedade distributiva a toda a expressão, remover aquele fator comum repetido e adicioná-lo multiplicando o polinômio inteiro. Abaixo você encontrará um exemplo do primeiro caso de que falamos (polinômio sem termo independente):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Extração dupla do fator comum
A extração de fatores comuns pode até ser feita extraindo fatores mais complexos, que incluem múltiplas variáveis. E você pode até extrair polinômios derivados da própria expressão principal. É importante não estabelecer limites quando se deseja realizar este tipo de operação, pois o objetivo da extração de fatores é simplificar ao máximo uma expressão algébrica .
Fatoração de polinômios usando identidades notáveis
Produtos notáveis podem nos ajudar a fatorar expressões polinomiais, uma vez que são expressões algébricas simplificadas. Portanto, ajudam-nos a passar diretamente de um polinómio longo para uma pequena fórmula composta por alguns termos. Portanto, é altamente recomendável aprender as fórmulas das identidades notáveis para poder identificar rapidamente quando você pode usá-las. E, portanto, economizando tempo com Ruffini ou qualquer outro método. A seguir, abordaremos as três regras que você precisa aprender:
- Diferença de quadrados: a² – b² = (a + b) · (a – b)
- Quadrado da soma: a² + 2ab + b² = (a + b)²
- Quadrado de subtração: a² – 2ab + b² = (a – b)²
Fatoração de polinômios por agrupamento
Em alguns casos podemos encontrar um polinômio de estrutura x² – ax – bx + ab , que pode ser simplificado removendo um fator comum: x (x – a) – b (x – a). E se tomarmos novamente o fator comum, ele pode ser ainda mais simplificado: (x – a) · (x – b). Portanto, as raízes deste polinômio seriam x = a e x = b. Como você pode ver, esse tipo de expressão algébrica possui uma estrutura muito fácil de fatorar e usar.
Exercícios de fatoração polinomial
Por fim, queremos oferecer uma série de exercícios para que você possa praticar a fatoração de polinômios. Assim você poderá internalizar melhor a teoria que explicamos hoje. Simplesmente, você deve resolver os exercícios em seu caderno e depois comparar os resultados com os que oferecemos a seguir.
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2