Esta página explica o que é uma função irracional, também chamada de função radical, bem como todas as características deste tipo de função. Você também descobrirá como calcular o domínio de funções radicais ou irracionais e, além disso, poderá ver como representá-las em um gráfico com exemplos e praticar com exercícios e problemas resolvidos passo a passo.
O que é uma função irracional (ou radical)?
Uma função irracional significa a mesma coisa que uma função radical e, portanto, compartilham uma definição:
Uma função irracional , também chamada de função radical , é uma função que possui a variável independente x sob o símbolo de uma raiz.
Como já sabemos, o resultado de uma raiz pode ser positivo ou negativo. Assim, a representação de uma função irracional (ou radical) tem duas curvas possíveis:
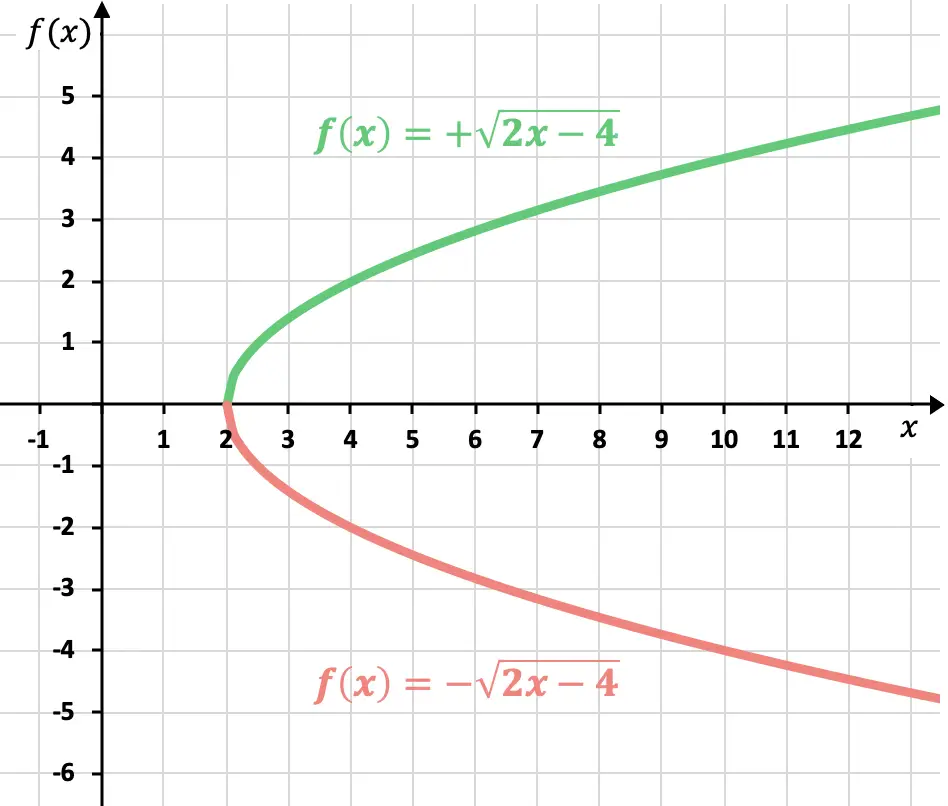
Mas se o sinal não for especificado, a função positiva deverá ser representada.
Por outro lado, uma função irracional não deve ser confundida com uma função racional. Embora tenham nomes muito semelhantes, são dois tipos de funções completamente diferentes.
Domínio de uma função irracional ou radical
O domínio de uma função com raízes depende da paridade do índice raiz, ou seja, depende se o índice radical é par ou ímpar.
Domínio de uma função com raiz de índice par
Como você bem sabe, não existe raiz (índice par) de um número negativo. Portanto, uma função radical com índice par existirá enquanto seu conteúdo for igual ou maior que 0.
Como exemplo, vejamos como é calculado o domínio da seguinte função radical ou irracional:
![]()
Esta é uma função de índice par radical, portanto devemos observar quando seu conteúdo é positivo ou zero :
![]()
Resolvemos a desigualdade:
![]()
Portanto a função existirá sempre que x for maior ou igual a 4, e é indicada pelo seguinte intervalo:
![]()
Domínio de uma função com raiz de índice ímpar
Funções irracionais com índice ímpar não apresentam esse problema, pois existe a raiz do índice ímpar de um número negativo:
![]()
Portanto, existem funções radicais de índice ímpar para qualquer valor de x . Ou, em outras palavras, o domínio consiste apenas em números reais .
Por exemplo, calcularemos o domínio de definição da seguinte função radical cujo índice é ímpar:
![]()
Por ser uma função irracional com índice ímpar, seu domínio consiste em números reais:
![]()
Como representar uma função irracional ou radical
Vamos ver como representar uma função com raízes em um gráfico usando um exemplo.
- Trace a seguinte função radical ou irracional em um gráfico:
![]()
A primeira coisa a fazer é encontrar o domínio da função. Por ser uma raiz quadrada, tudo o que contém deve ser positivo, pois não existe raiz quadrada de um número negativo. Portanto, a função radical existirá enquanto seu conteúdo for igual ou maior que 0:
![]()
![]()
Assim, o domínio da função consiste em todos os números maiores ou iguais a -2. Isso é para dizer:
![]()
Depois de conhecermos o domínio da função, criamos uma tabela de valores. Obviamente, quanto mais pontos calcularmos, mais precisa será a representação da função. Mas calcular 3 ou 4 pontos no intervalo do domínio é suficiente:
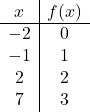
Representamos agora os pontos obtidos em um gráfico :
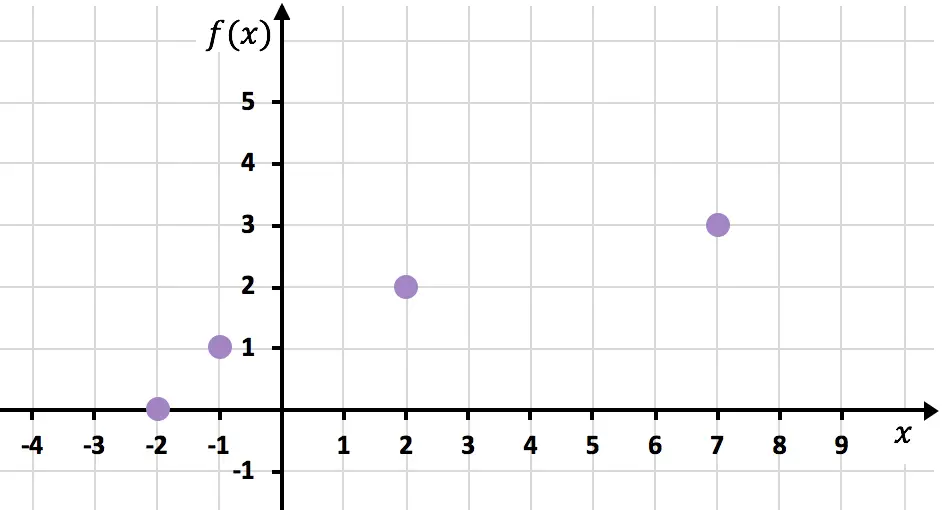
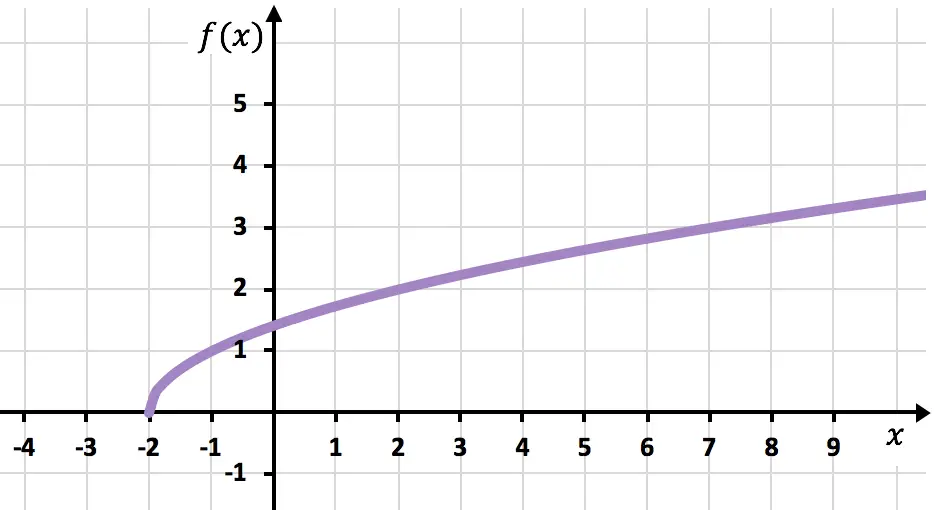
E finalmente, juntamos os pontos e estendemos a curva para indicar que a função continua a crescer:
Exercícios resolvidos sobre funções irracionais ou radicais
Exercício 1
Encontre o domínio da seguinte função radical:
![]()
A raiz quadrada de um número negativo não existe. Portanto, a função existirá quando o argumento raiz for positivo ou zero:
![]()
![]()
![]()
![]()
![]()
Exercício 2
Encontre o domínio da seguinte função irracional:
![]()
A raiz quadrada de um número negativo não tem solução real. Portanto, a função existirá enquanto o conteúdo da raiz for positivo ou zero:
![]()
![]()
![]()
Lembre-se que se numa inequação mudarmos os lados de um número negativo que se multiplica ou divide, devemos também rodar o sinal da inequação.
![]()
![]()
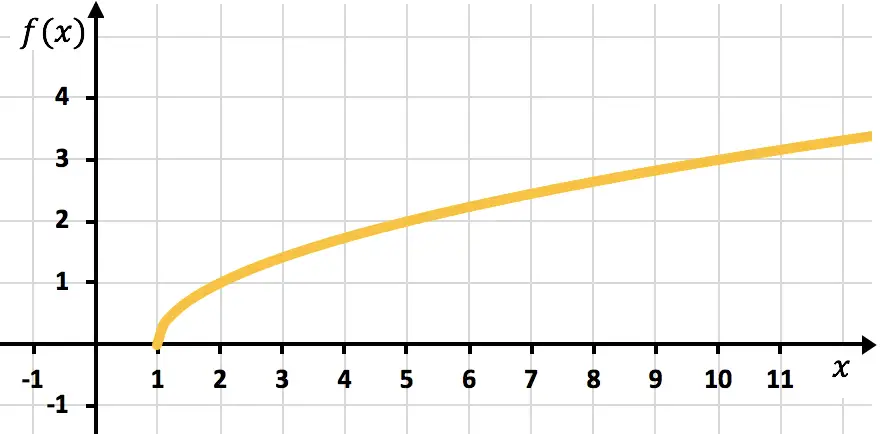
Exercício 3
Trace a seguinte função irracional em um gráfico:
![]()
Primeiramente devemos calcular o domínio da função:
![]()
![]()
![]()
Agora criamos um array de valores fornecendo os valores da função no intervalo do domínio:
![]()
![]()
![]()
![]()

Por fim, traçamos os pontos e traçamos a função no gráfico:
Exercício 4
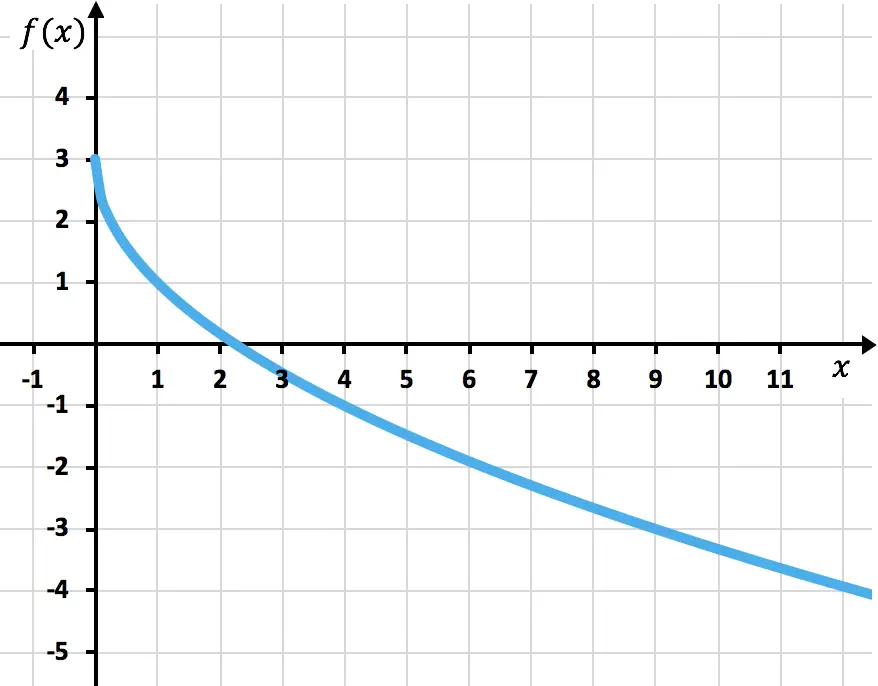
Faça um gráfico da seguinte função irracional ou radical:
![]()
Primeiramente devemos calcular o domínio da função:
![]()
![]()
Agora criamos um array de valores fornecendo os valores da função no intervalo do domínio:
![]()
![]()
![]()
![]()

Por fim, plotamos os pontos e desenhamos a função no gráfico:
Exercício 5
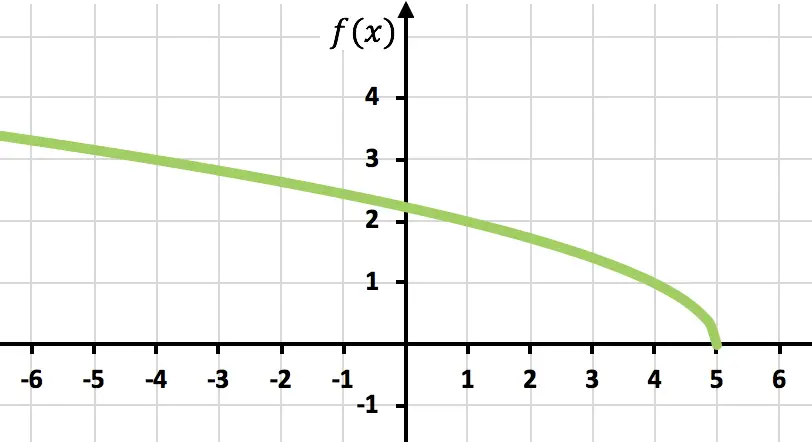
Faça um gráfico da seguinte função irracional ou radical:
![]()
Antes de traçar a função, precisamos calcular o domínio da função:
![]()
![]()
![]()
Lembre-se que se numa desigualdade mudarmos os lados de um número negativo que se multiplica ou divide, devemos também mudar o sinal da desigualdade.
![]()
![]()
Agora construímos uma tabela de valores avaliando a função em pontos que pertencem ao domínio da função:
![]()
![]()
![]()
![]()

E por fim, basta representar os pontos e pintar a função no gráfico:
Exercício 6
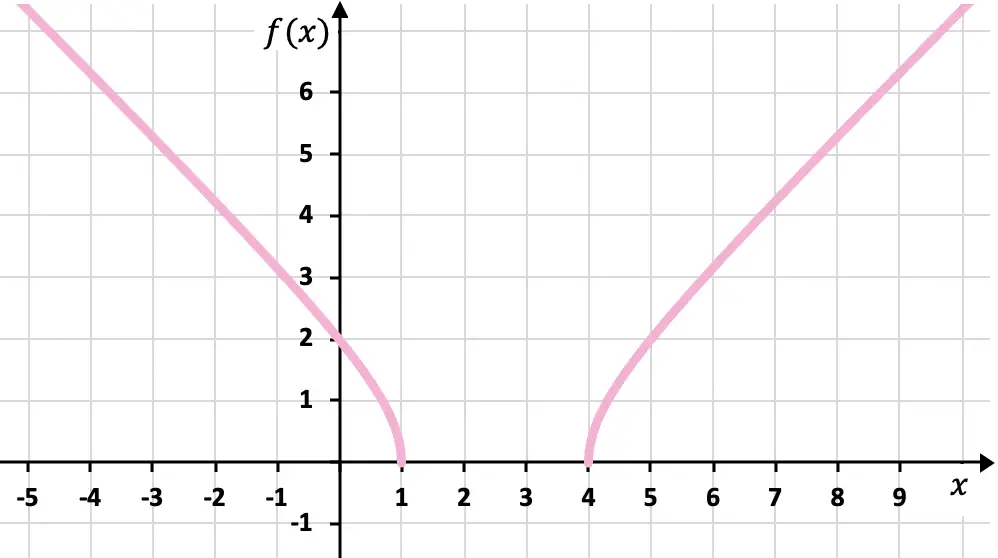
Trace a seguinte função irracional ou radical em um gráfico:
![]()
Devemos primeiro calcular o domínio da função:
![]()
Neste caso, obtivemos uma desigualdade de segundo grau, então precisamos aplicar a fórmula das equações quadráticas para resolvê-la:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3e5bc09c561e2790b1af96a618a015a0_l3.png)
Dividimos a linha em três pedaços com as raízes obtidas:

E substituímos um número por cada seção da desigualdade, para ver quais seções satisfazem a desigualdade e, portanto, pertencem ao domínio:
![x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”></p>
</p>
<p>❌</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9c9c5a39dc152cdcb902dbf0b2e5b59_l3.png)
![]()
![]()
✅
Assim, as seções que respeitam a desigualdade são as dos lados:

O domínio da função é portanto:
![]()
Depois de calcularmos o domínio da função, construímos uma tabela de valores fornecendo os valores da função no intervalo do domínio:
![]()
![]()
![]()
![]()
![]()
![]()

Por fim, representamos os pontos obtidos no gráfico e traçamos a função:
Exercício 7
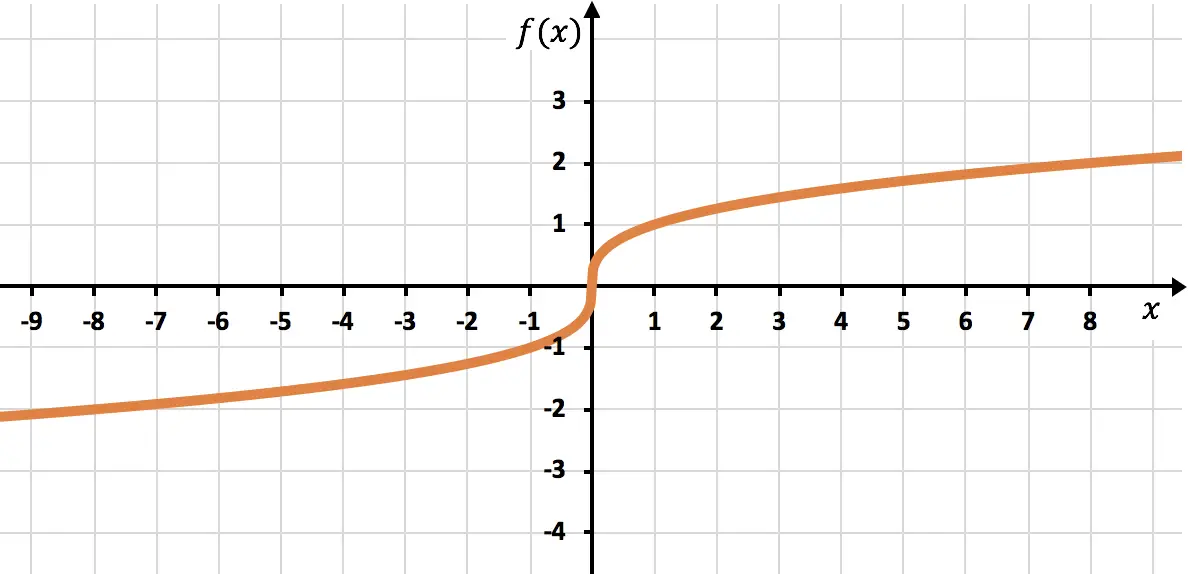
Represente no gráfico a seguinte função formada por uma raiz:
![]()
É uma função irracional cuja raiz possui índice ímpar, portanto o domínio da função consiste em números reais:
![]()
Podemos, portanto, tomar qualquer ponto para criar a tabela de valores. Neste caso procuraremos muitos pontos porque é uma raiz cúbica:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Por fim, traçamos os pontos encontrados e traçamos a função no gráfico:
Exercício 8
Resolva o seguinte problema relacionado a funções irracionais (ou radicais):
O consumo da bateria de um celular é dado pela seguinte função:
![]()
Onde o consumo é expresso em miliamperes (mA) e
![]()
é o tempo decorrido em minutos.
Determine o valor da constante
![]()
para que após 4 minutos o consumo seja de 35 mA.
Que após 4 minutos o consumo seja de 35 mA significa que quando t é 4, f(t) é 35. Então f(4)=35.
![]()
![]()
Agora precisamos resolver a equação que obtivemos. Se você olhar de perto, é uma equação irracional, pois tem uma raiz. Neste tipo de equações a primeira coisa a fazer é isolar a raiz de um lado, que neste caso já está isolada. Uma vez isolados, devemos elevar ambos os lados da equação ao quadrado:
![]()
Então simplificamos a raiz:
![]()
E resolvemos a equação:
![]()
![]()
![]()
Finalmente, em equações irracionais, as soluções devem ser verificadas. Devemos, portanto, substituir K=-1221 na equação do início:
![]()
![]()
![]()
![]()
Como a igualdade é satisfeita, K=-1221 é uma solução.