Nesta página você encontrará a explicação do que são pontos alinhados. Você também verá todos os métodos disponíveis para determinar se 3 (ou mais) pontos estão alinhados. E mais, você encontrará diversos exemplos e até exercícios resolvidos para praticar.
O que significa que os pontos estão alinhados?
Na geometria analítica, três ou mais pontos estão alinhados se estiverem todos na mesma linha, ou seja, se puderem ser unidos traçando uma linha reta entre eles.
Obviamente, 2 pontos estarão sempre alinhados, pois você sempre pode traçar uma linha entre dois pontos. No entanto, três pontos não precisam estar na mesma linha. Principalmente, existem dois métodos para saber se 3 ou mais pontos estão alinhados:
- Método vetorial : consiste em ver se os vetores que formam os pontos são proporcionais.
- Método de equação de linha : consiste em determinar se os pontos pertencem à mesma linha.
Abaixo está a explicação de cada procedimento e exemplos para que você decida qual é o melhor para você.
Como saber se 3 (ou mais) pontos estão alinhados com o método vetorial
Considerando três pontos:
![]()
Os três pontos estão alinhados se os vetores
![]()
E
![]()
eles têm a mesma direção, ou seja, se seus componentes são proporcionais.
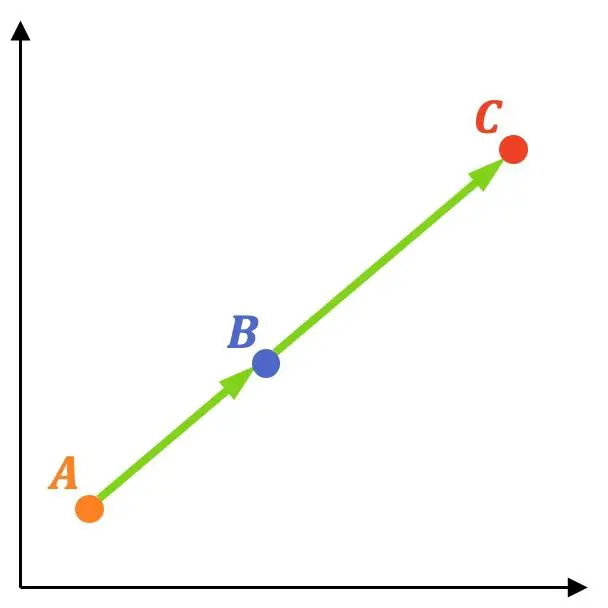
Vejamos um exemplo de como isso é feito:
- Determine se os três pontos a seguir estão alinhados:
![]()
Primeiro, calculamos os vetores entre os pontos. Basta calcular dois vetores diferentes:
![]()
![]()
E então verificamos se as coordenadas dos vetores são proporcionais:
![]()
Ao dividir as componentes X e as componentes Y dos dois vetores obtemos o mesmo resultado (-2), pois os vetores têm a mesma direção e, portanto, os pontos estão alinhados .
Este método também pode ser utilizado para saber se três ou mais pontos estão alinhados no espaço (em R3), bastando somar é verificar se a terceira componente dos dois vetores (componente Z) também é proporcional.
Se este artigo for útil para você, provavelmente também terá interesse em saber como calcular o ponto médio entre dois pontos , pois, obviamente, encontrar o ponto médio de 2 pontos é uma forma de determinar um terceiro ponto alinhado com os outros dois pontos. Você pode ver como isso é feito na página do link, além disso você também poderá ver exemplos e exercícios resolvidos passo a passo.
Como saber se 3 (ou mais) pontos estão alinhados com o método da equação da linha reta
Como acabamos de ver na seção anterior, uma forma de estudar o alinhamento de 3 ou mais pontos é utilizar os vetores que podem se formar entre eles. Bem, outro método é começar com a equação de uma reta:
Considerando três pontos:
![]()
Os três pontos estão alinhados se todos pertencerem à mesma linha. Portanto, para saber se três ou mais pontos estão alinhados, devem ser seguidos os seguintes passos:
- Encontre a equação da reta que passa por dois dos três pontos.
- Verifique se o terceiro ponto também pertence à linha. Neste caso significa que os 3 pontos estão alinhados, porém se a condição não for atendida significa que os pontos não estão alinhados.
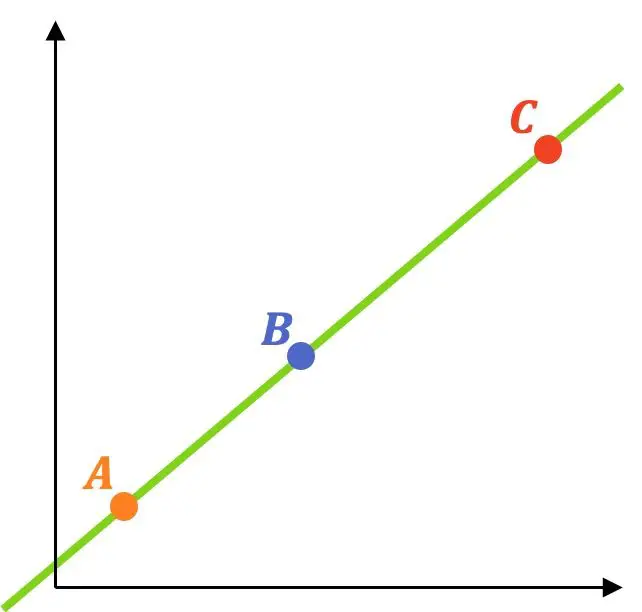
Como exemplo, resolveremos um exercício utilizando este método:
- Verifique se os três pontos a seguir estão alinhados:
![]()
Em primeiro lugar, devemos calcular a equação da reta que passa pelos pontos A e B. Portanto, encontramos o vetor diretor da reta:
![]()
Agora você tem que construir a equação da reta, você pode escolher o tipo que deseja: paramétrico, implícito, geral, etc. Mas neste caso usaremos a equação contínua. Portanto, a equação contínua da reta que passa pelo ponto A e pelo ponto B será:
![]()
Assim que tivermos a equação da reta, devemos verificar se o outro ponto também pertence à mesma reta. Para fazer isso, substituímos as coordenadas do ponto C na equação da reta:
![]()
![]()
![]()
Empatamos, então o ponto satisfaz a equação da reta. E portanto os 3 pontos são colineares .
Ressalta-se que um conjunto de pontos alinhados não precisa ser equidistante, ou seja, a distância entre vários pontos alinhados pode ser diferente. Você pode ver a diferença entre os dois conceitos na explicação da distância entre dois pontos (geometria) , onde também pode ver exemplos e exercícios resolvidos passo a passo.
Exercícios resolvidos de pontos alinhados
Exercício 1
Determine se os três pontos a seguir estão alinhados:
![]()
Podemos escolher um dos dois métodos que vimos para resolver o problema. Neste caso usaremos o método vetorial.
Primeiro, calculamos os vetores entre os pontos:
![]()
![]()
E agora verificamos se as coordenadas cartesianas dos vetores são proporcionais:
![]()
Ao dividir as componentes X e as componentes Y dos dois vetores entre si obtemos o mesmo resultado (-4), portanto os vetores têm a mesma direção. Fato que indica que os pontos estão alinhados .
Exercício 2
Dados 3 pontos:
![]()
Determine quais deles se alinham com os dois pontos a seguir:
![]()
Neste caso utilizaremos o método da equação da reta, assim salvaremos alguns cálculos.
Calculamos, portanto, a equação contínua da reta que passa pelos pontos D e E:
![]()
![]()
E agora vamos verificar quais pontos correspondem à equação da reta e, portanto, estão alinhados com os pontos D e E, e quais não estão.
Verificamos o ponto A:
![]()
![]()
![]()
A equação da reta não é verdadeira, então o ponto A não está alinhado com os pontos D e E.
Agora verificamos o ponto B:
![]()
![]()
![]()
Neste caso a equação da reta é cumprida, então o ponto B é colinear com os pontos D e E.
E por fim, repetimos o processo com o ponto C:
![]()
![]()
![]()
A equação da reta não é verdadeira, então o ponto C não está alinhado com os pontos D e E.
Exercício 3
Encontrando o valor do desconhecido
![]()
para que os 3 pontos a seguir estejam alinhados:
![]()
Neste caso usaremos o método vetorial.
Tentamos, portanto, calcular os vetores entre os pontos:
![]()
![]()
Para que a colinearidade de três pontos seja satisfeita, as coordenadas dos dois vetores devem ser proporcionais. Portanto, aplicamos esta condição:
![]()
E resolvemos a equação:
![]()
![]()
![]()
![]()
![]()
![]()
Então para que os 3 pontos fiquem alinhados
![]()
deve valer 2.