Esta página explica o que é uma função quadrática bem como todas as suas características: curvatura, vértice, pontos de intersecção com os eixos, etc. Você também aprenderá como representar uma função quadrática em um gráfico. E por fim, você pode praticar com exemplos, exercícios passo a passo e problemas sobre funções quadráticas.
O que é uma função quadrática?
A definição de uma função quadrática é a seguinte:
Em matemática, uma função quadrática (ou parabólica) é uma função polinomial de grau 2, ou seja, uma função em que o termo de maior grau é de segundo grau. Portanto, a fórmula para uma função quadrática é:
![]()
Ouro:
-
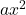
é o termo quadrático.
-
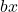
é o termo linear.
-

é o termo independente.
O domínio de uma função quadrática sempre consiste em números reais.
![]()
Concavidade e convexidade de uma função quadrática
Analisar a curvatura de uma função quadrática ou parabólica é muito simples, pois depende apenas do coeficiente quadrático.
- Se o coeficiente

é positiva, a função quadrática é convexa (na forma

). A cimeira é, portanto, um mínimo.
- Se o coeficiente

é negativo, a função quadrática é côncava (em forma

). O pico é, portanto, um máximo.


Nota: A comunidade matemática ainda não concorda plenamente e, por isso, alguns professores dizem o contrário: chamam uma função côncava aquela que tem a forma de um
![]()
, e uma função convexa que tem a forma de
![]()
. Em todo caso, o importante é qual forma tem a função, seja qual for o nome.
Vértice de uma função quadrática
Para representar graficamente uma função quadrática, é necessário conhecer as coordenadas do vértice da parábola.
Para encontrar o vértice de uma função quadrática, precisamos calcular a coordenada X do ponto usando a seguinte fórmula:
![]()
Então podemos encontrar a outra coordenada do vértice calculando a imagem da função naquele ponto:
![]()
Assim, as coordenadas do vértice de uma função quadrática (ou parábola) são:
![]()
Cortando pontos com os eixos de uma função quadrática
Uma parábola sempre intercepta o eixo y (eixo Y), e isso acontece quando
![]()
Portanto, para calcular o ponto de corte de uma função quadrática com eixo Y, deve-se resolver
![]()
Por exemplo, o ponto de intersecção com o eixo OY da seguinte função quadrática é:
![]()
![]()
![]()
Por outro lado, o ponto de corte de uma função quadrática com o eixo x (eixo X) ocorre quando
![]()
Então para calcular o ponto de intersecção com o eixo X você tem que resolver a equação
![]()
A título de exemplo, segue abaixo o cálculo do ponto de corte com o eixo OX da mesma função quadrática:
![]()
![]()
Resolvemos a equação quadrática com a fórmula geral:
![]()
![]()
O ponto de intersecção da função quadrática com o eixo X é, portanto:
![]()
Neste caso, obtivemos apenas uma solução para a equação quadrática, mas poderíamos ter obtido duas soluções. Neste caso, isso significa que a função quadrática intercepta o eixo X em dois pontos diferentes.
Exemplo de representação de uma função quadrática ou parabólica
Vamos ver como representar uma função quadrática em um gráfico usando um exemplo.
- Faça um gráfico da seguinte função:
![]()
A primeira coisa a fazer é calcular o vértice da parábola. Para fazer isso, usamos a fórmula que vimos acima:
![]()
Depois de sabermos onde estará o vértice, precisamos construir uma tabela de valores: Calculamos o valor da função no vértice e nos pontos que o rodeiam:
![]()
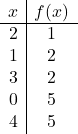
Você também pode calcular os pontos de corte da função quadrática com os eixos cartesianos para desenhar melhor a parábola, mas isso não é estritamente necessário.
Representamos agora os pontos obtidos em um gráfico :
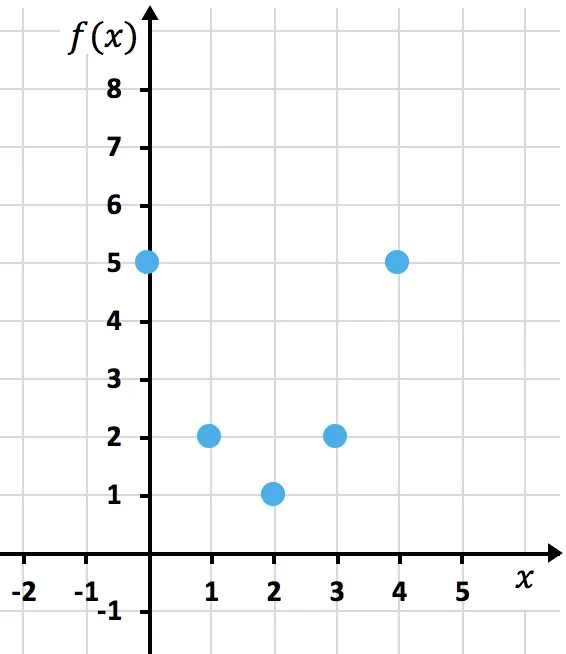
E por fim, juntamos os pontos formando a parábola. Depois alongamos os ramos da parábola para indicar que ela continua para cima:

Exercícios resolvidos sobre funções quadráticas
Exercício 1
Encontre o vértice da seguinte função quadrática:
![]()
Primeiro calculamos a coordenada X do vértice usando a fórmula:
![]()
E agora calculamos a outra coordenada avaliando a função no ponto:
![Rendered by QuickLaTeX.com \begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6067325564a5af06f7384d76157f3aa_l3.png)
O vértice da função quadrática é, portanto:
![]()
Exercício 2
Encontre os pontos de corte da seguinte função com os eixos:
![]()
Para calcular o ponto de corte com o eixo Y, precisamos calcular
![]()
![]()
A função, portanto, passa pelo eixo Y no ponto:
![]()
E para encontrar os pontos de corte com o eixo X precisamos resolver
![]()
![]()
![]()
Calculamos as raízes da equação quadrática com a fórmula:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d909ba6581faf5916f0b1c0df7e471f_l3.png)
A função, portanto, corta o eixo X em dois pontos:
![]()
Exercício 3
Faça um gráfico da seguinte função quadrática:
![]()
Esta é uma função quadrática. conseqüentemente, para representá-la deve-se primeiro calcular a abcissa do vértice da parábola com a fórmula:
![]()
Agora criamos a tabela de valores. Para fazer isso, calculamos o valor de
![]()
no topo e ao redor do topo:
![]()
![]()
![]()
![]()
![]()
E por fim, plotamos os pontos no gráfico e desenhamos a parábola:

Exercício 4
Faça um gráfico da seguinte função quadrática:
![]()
Esta é uma função de segunda ordem. conseqüentemente, para representá-la você deve primeiro encontrar a abcissa do vértice da parábola com a fórmula:
![]()
Agora construímos a tabela de valores. Para fazer isso, calculamos o valor de
![]()
no topo e ao redor do topo:
![]()
![]()
![]()
![]()
![]()

Por fim, plotamos os pontos no gráfico e desenhamos a parábola:

Exercício 5
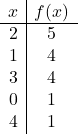
Trace a seguinte função quadrática incompleta em um gráfico:
![]()
É uma função polinomial de grau dois. conseqüentemente, para representá-la deve-se primeiro calcular a abcissa do vértice da parábola com a fórmula:
![]()
Nesse caso, a função está incompleta, pois não possui termo de primeiro grau. Por isso
![]()
Agora fazemos a tabela de valores. Para fazer isso, calculamos o valor de
![]()
no topo e ao redor do topo:
![]()
![]()
![]()
![]()
![]()

Por fim, plotamos os pontos no gráfico e desenhamos a parábola:

Exercício 6
Resolva o seguinte problema relacionado a funções quadráticas:
O custo de produção de um produto é definido pela seguinte função:
![]()
Ouro
![]()
são as unidades produzidas (em milhares) e
![]()
é o custo de produção das unidades (em milhares de euros).
- Representa a função de custo de produção em um gráfico.
- Determine quantos milhares de unidades devem ser produzidas para minimizar custos.
Esta é uma função quadrática. conseqüentemente, para representá-la você deve primeiro encontrar a abcissa do vértice da parábola com a fórmula:
![]()
Agora fazemos a tabela de valores. Para fazer isso, calculamos o valor de
![]()
no topo e ao redor do topo:
![]()
![]()
![]()
![]()
![]()
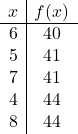
Agora plotamos os pontos no gráfico e desenhamos a parábola:
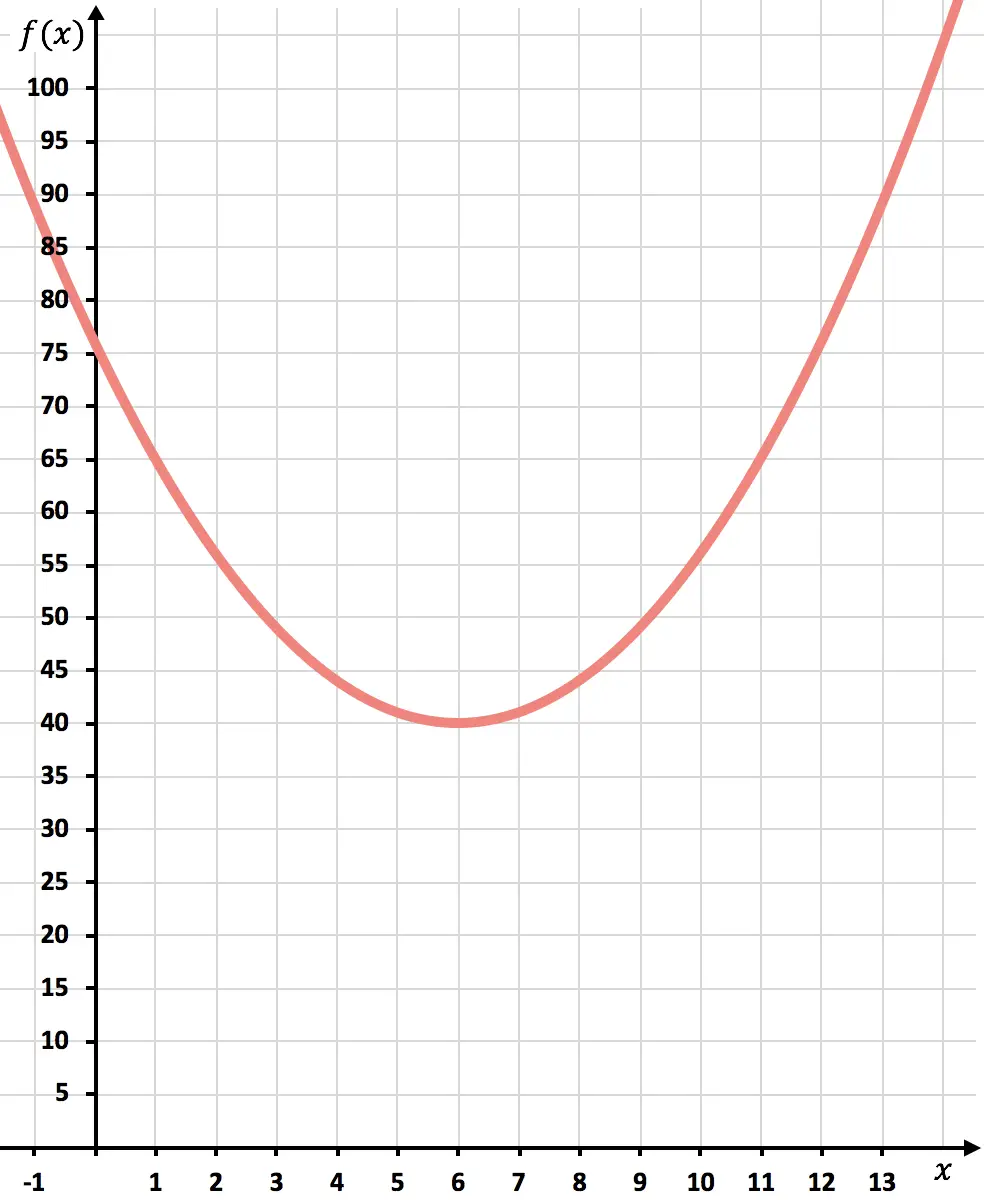
Uma vez representada a função, veremos o quanto os custos são minimizados.
Como mostra o gráfico, os custos mínimos serão alcançados no topo da parábola. Porque é aí que a função assume o menor valor.
Concluindo, os custos serão minimizados com a produção de 6.000 unidades.
Exercício 7
Resolva o seguinte problema de função quadrática:
Um atleta realiza um lançamento de dardo cuja trajetória pode ser representada pela seguinte função:
![]()
Ouro
![]()
são os metros percorridos pelo dardo e
![]()
sua altura (também em metros).
Qual é a altura máxima que o dardo pode atingir?
Esta é uma função quadrática, portanto a trajetória do dardo será uma parábola.
Além disso, como o coeficiente do termo quadrático é negativo (-0,025), a parábola terá formato de U invertido e seus ramos serão descendentes. Assim o dardo atingirá a altura máxima no topo, pois este será o ponto mais alto da parábola.
Portanto, calculamos a abcissa do vértice da parábola com a fórmula:
![]()
E então calculamos a altura do dardo naquele ponto, avaliando a função em
![]()
![]()
A altura máxima que o dardo pode atingir é, portanto, de 42 metros.
Exercício 8
Resolva o seguinte problema relativo a funções quadráticas:
Os custos de produção (em euros) de uma empresa são definidos pela seguinte função:
![]()
Ouro
![]()
são as unidades produzidas.
E o preço de venda de cada unidade é de 520€.
- Quanto lucro a empresa terá se vender 150 unidades?
- Quantas unidades devem ser vendidas para obter lucro máximo?
A empresa ganha 520€ por cada unidade vendida. Portanto, a função que define a renda é:
![]()
Ouro
![]()
são as unidades vendidas.
Mas nos perguntam sobre o lucro, ou seja, a renda menos os custos. Subtraímos, portanto, a receita menos os custos para obter a função que descreve o lucro da empresa:
![]()
![]()
![]()
![]()
Uma vez conhecida a função que descreve o lucro da empresa, basta substituir 150 na expressão da função para calcular o lucro que a empresa obterá com a venda de 150 unidades:
![Rendered by QuickLaTeX.com \begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f5e6f3101145bcf1a2ece4db3e07c4e_l3.png)
Assim, ao vender 150 unidades, a empresa terá um lucro de 12.500€.
O comunicado também nos pede para calcular em quantas unidades o lucro máximo é alcançado.
A função que descreve o lucro é uma função quadrática, portanto terá o formato de uma parábola. E como o coeficiente do termo quadrático é negativo (-1), a parábola terá formato de U invertido e seus ramos irão para baixo. Portanto, os ganhos máximos serão obtidos no topo, já que este é o ponto mais alto da parábola.
Portanto, calculamos a abcissa do vértice da parábola com a fórmula:
![]()
Assim, a empresa obterá o lucro máximo com a venda de 250 unidades.
Por outro lado, mesmo que o comunicado não o solicite, podemos determinar o lucro que será obtido com a venda destas 250 unidades:
![]()
€