Valor numérico de um polinômio

Nesta página você descobrirá o que é e como calcular o valor numérico de um polinômio. Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo do valor numérico de um polinômio.

Qual é o valor numérico de um polinômio?

Em matemática, o valor numérico de um polinômio P(x) para o valor x=a, ou seja P(a), é o resultado obtido substituindo a variável x do polinômio pelo número a e realizando os cálculos indicados na expressão polinomial.

Para que você entenda melhor o conceito de valor numérico de um polinômio, mostramos a seguir como ele é calculado com um exemplo:

Como calcular o valor numérico de um polinômio

Agora que conhecemos a definição matemática do valor numérico de um polinômio, vamos ver como determinar o valor numérico de um polinômio usando um exemplo:

  • Qual é o valor numérico do seguinte polinômio para x=2?

P(x)=x^3+5x^2-4x+1

Para encontrar o valor numérico do polinômio é necessário avaliar o referido polinômio no valor dado pelo problema, ou seja, é necessário substituir a variável

x

do polinômio pelo valor da instrução. Portanto, neste caso precisamos substituir a letra

x

Para 2:

P(2)=2^3+5\cdot 2^2-4\cdot 2+1

E assim que substituirmos o valor na expressão algébrica do polinômio, realizamos as operações. Então primeiro resolvemos para as potências:

P(2)=8+5\cdot 4-4\cdot 2+1

Agora calculamos as multiplicações:

P(2)=8+20-8+1

E finalmente, adicionamos e subtraímos os termos:

\bm{P(2)=21}

Concluindo, o valor numérico do polinômio para x=2 é igual a 21.

Como você pode ver, encontrar o valor numérico de um polinômio não é muito complicado, mas tem algumas aplicações muito úteis. Por exemplo, saber encontrar o valor numérico de um polinômio é essencial para poder usar o teorema do resto, um teorema muito importante sobre polinômios. Clique neste link e descubra o que é o teorema do resto , você encontrará sua explicação, exemplos de uso e exercícios resolvidos passo a passo.

Exemplos de valores numéricos de polinômios

Para que você entenda como obter o valor numérico de um polinômio, deixamos outros exemplos resolvidos:

Exemplo 1

  • Calcule o valor numérico do polinômio

    P(x)=x^3-2x^2+3x+6

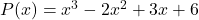
    Para

    x=-1.

\begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}

Neste caso, o valor numérico do polinômio é igual a 0. Isso tem consequências devido às propriedades dos polinômios, pois graças ao teorema do fator podemos saber qual será o resto de certas divisões entre polinômios. Para saber mais, clique no link anterior, onde explicamos o que é e para que serve esse teorema.

Exemplo 2

  • Determine o valor numérico do polinômio

    P(x)=-2x^3+7x^2-8x-2

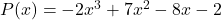
    Para

    x=3.

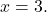
\begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}

Até agora vimos apenas como determinar o valor numérico de um polinômio da maneira clássica, mas você deve saber que existe outro método. Mais especificamente, você também pode calcular o valor numérico de um polinômio com o método Ruffini . Você também deve saber como utilizar este procedimento, por isso recomendamos conferir sua explicação detalhada no link.

Valor numérico de um polinômio com duas ou mais variáveis

Acabamos de ver como determinar o valor numérico de um polinômio quando ele possui apenas uma variável. Mas… como obter o valor numérico de um polinômio quando ele possui mais de uma variável?

Pois bem, se um polinômio possui 2 ou mais letras, seu valor numérico deve ser calculado da mesma forma, ou seja, primeiro substitua cada variável do polinômio pelo seu valor correspondente e depois resolva as operações polinomiais .

Como exemplo, você tem um problema desse tipo resolvido abaixo:

  • Encontre o valor numérico do polinômio multivariado

    P(x,y)=x^2y+4xy-2x^2+6y-5

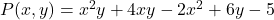
    para os valores

    x=2, y=3.

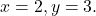
Primeiro, substituímos cada variável pelo seu valor correspondente, ou seja, substituímos a letra

x

por 2 e mudamos a letra

y

por 3:

P(2,3)=2^2\cdot 3+4\cdot 2\cdot 3-2\cdot 2^2+6\cdot 3-5

Resolvemos para as potências:

P(2,3)=4\cdot 3+4\cdot 2\cdot 3-2\cdot 4+6\cdot 3-5

Agora calculamos os produtos:

P(2,3)=12+24-8+18-5

E por fim fazemos as adições e subtrações:

\bm{P(2,3)=41}

Portanto, o valor numérico do polinômio para os dados da instrução é equivalente a 41.

Exercícios resolvidos sobre o valor numérico de um polinômio

Exercício 1

Qual é o valor numérico do polinômio P(x) para x=-2?

P(x)=-2x^3-4x^2+3x+8

Para encontrar o valor numérico do polinômio, precisamos simplesmente substituir o valor dado na declaração na expressão polinomial e resolver as operações resultantes:

\begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}

Exercício 2

Calcule o valor numérico do seguinte polinômio com frações para x=4.

P(x)=\cfrac{1}{2} x^2-\cfrac{5}{4}x + 7

Quer o polinômio tenha frações ou não, o procedimento para encontrar o valor numérico do polinômio é sempre o mesmo. Devemos portanto substituir a variável x por 4 e resolver os cálculos:

\begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}

Exercício 3

Determine o valor numérico do polinômio para os valores x=3, y=5 e z=-2

P(x,y,z)=x^2yz+4y^2z^2-3x^2z+6xyz

Para determinar o valor numérico de um polinômio multivariado, basta substituir os valores dados no problema na expressão algébrica e resolver as operações resultantes:

\begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}

Exercício 4

Dado o polinômio

P(x)= -2x^3-3x^2+5x+k

calcular o valor do parâmetro

k

para que

P(-2)=5.

Neste problema, para encontrar o valor da incógnita

k

precisamos resolver a equação

P(-2)=5.

P(-2)=5

Portanto, primeiro tentamos calcular o valor de P(-2):

\begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}

Agora igualamos a expressão obtida a 5:

P(-2)=5

-6+k=5

E finalmente, resolvemos a equação resultante:

k=5+6

\bm{k=11}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima