Nesta página explicamos como aplicar a regra de Ruffini para dividir polinômios. Além da explicação, você poderá ver exemplos e exercícios resolvidos passo a passo sobre divisões de polinômios com a regra de Ruffini. Além disso, você encontrará todas as aplicações deste método e, de fato, mais de uma certamente o surpreenderá.
Qual é a regra de Ruffini?
Em matemática, a regra de Ruffini é um método algébrico que permite dividir rapidamente qualquer polinômio por polinômios da forma xr . A regra de Ruffini leva o nome do matemático Paolo Ruffini, que inventou este método.
No entanto, a regra de Ruffini não é usada apenas para dividir polinômios, ela tem muitos outros usos. Por exemplo, a regra de Ruffini também é usada para encontrar as raízes de um polinômio, para encontrar o valor numérico de um polinômio, para fatorar um polinômio ou mesmo para resolver equações de terceiro grau ou superiores. A seguir veremos como se aplica a regra de Ruffini para poder realizar todas essas operações.
Finalmente, a regra de Ruffini também é conhecida como método de Ruffini, teorema de Ruffini ou divisão sintética de polinômios.
Como aplicar a regra de Ruffini
Como vimos, o principal uso da regra de Ruffini é dividir um polinômio por um binômio, ou seja, fazer uma divisão do seguinte tipo:
![]()
Observe que para utilizar a regra de Ruffini , o polinômio divisor deve ser sempre formado por um x (com coeficiente igual a 1) e um número (positivo ou negativo), caso contrário o algoritmo de Ruffini não poderá ser utilizado.
Para aplicar a regra de Ruffini, todo um procedimento deve ser seguido, então a seguir resolveremos um exemplo passo a passo para ver como a regra de Ruffini (ou método de Ruffini) é aplicada.
Exemplo de regra de Ruffini
- Resolva a seguinte divisão de polinômios usando a regra de Ruffini:
![]()
Primeiro de tudo você precisa desenhar duas linhas perpendiculares que se cruzam e, em seguida, colocar o dividendo e o divisor da seguinte forma:
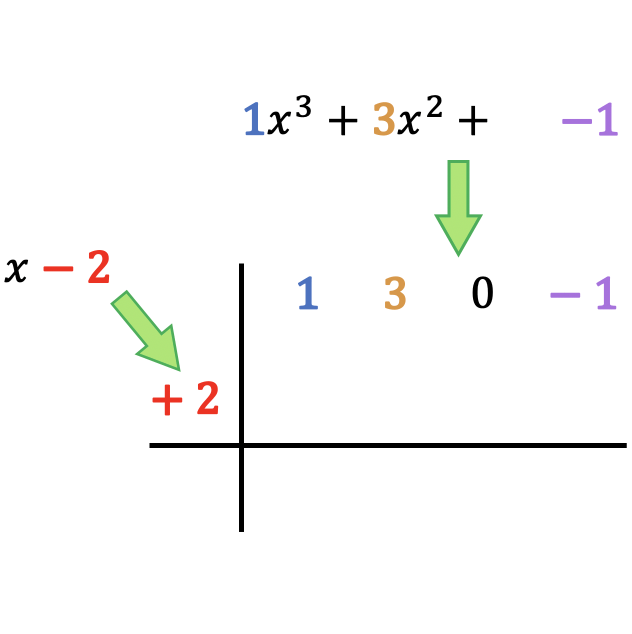
Como você pode ver, devemos colocar os coeficientes do polinômio dividendo no topo, ordenados do grau mais alto para o mais baixo, e colocamos o termo independente do polinômio divisor à esquerda da caixa com mudança de sinal .
Atenção: Se o polinômio do dividendo não possuir um termo de determinado grau (polinômio incompleto), é colocado 0 em seu lugar. Por exemplo, neste caso o polinômio
![]()
Não possui monômio de grau 1, então colocamos 0 em seu lugar.
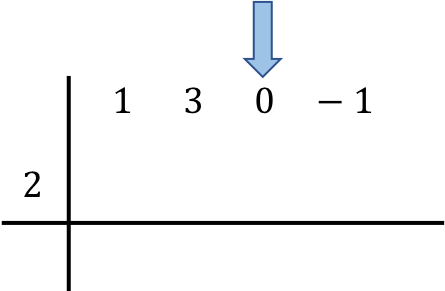
Depois de posicionarmos os polinômios envolvidos na operação, baixamos o primeiro número diretamente para a linha abaixo:
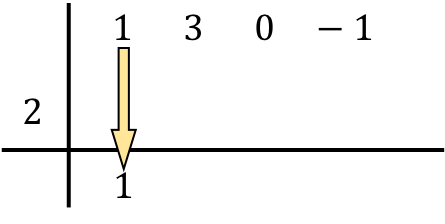
Agora vem a etapa que caracteriza a regra de Ruffini: multiplicamos o número abaixo pelo número da esquerda e colocamos o resultado na seguinte coluna :
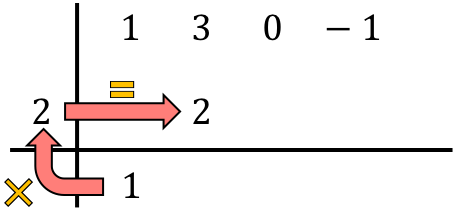
E somamos os números da coluna, colocando o resultado da soma logo abaixo:
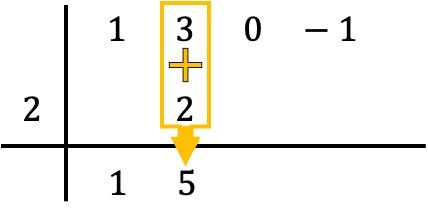
Então, o método de Ruffini envolve repetir esse processo. Então fazemos a mesma coisa novamente: multiplicamos o número de baixo pelo número da esquerda, colocamos o resultado na próxima coluna e, por fim, somamos os números que estão alinhados verticalmente:
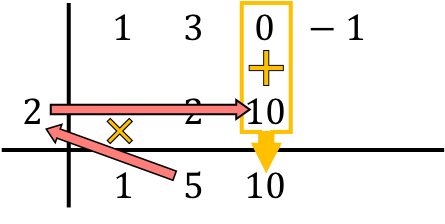
E repetimos o mesmo procedimento sucessivamente até o final. Primeiro fazemos o produto do número abaixo pelo número da esquerda, depois colocamos o resultado na próxima coluna e, por fim, somamos os números da mesma coluna:
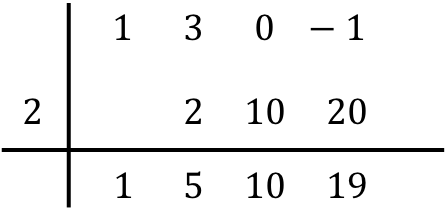
Então, quando tivermos preenchido todas as colunas, isso significa que terminamos de dividir os polinômios.
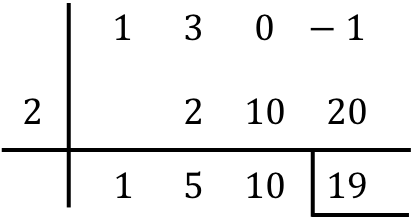
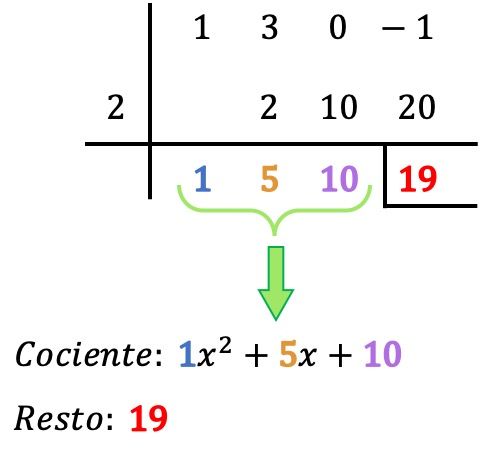
Então você só precisa encontrar o resultado da divisão dos polinômios:
- O resto da divisão entre os dois polinômios é o último número da linha abaixo, portanto no nosso caso o resto é igual a 19. O resto geralmente é indicado colocando uma barra à esquerda e outra abaixo do referido número.
- O quociente da divisão polinomial é determinado pelos demais valores obtidos, que são os coeficientes do quociente polinomial. O primeiro dígito da direita corresponde ao coeficiente da nota 0 do período, o próximo dígito é o coeficiente da nota 1 do período, o próximo à nota 2, o próximo à nota 3,… e assim sucessivamente até o final. . ENTÃO:
Exercícios resolvidos da regra de Ruffini
Abaixo você encontrará vários exercícios resolvidos passo a passo sobre a regra de Ruffini para que você possa praticar e entender como resolver divisões de polinômios com este método. Recomendamos que você experimente cada exercício e depois verifique se fez corretamente olhando a correção.
Exercício 1
Execute a seguinte divisão de polinômios com a regra de Ruffini:
![]()
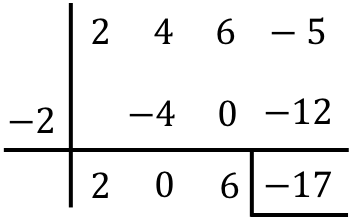
O resultado da divisão entre os dois polinômios é, portanto:
Quociente:
![]()
Descansar:
![]()
Exercício 2
Calcule a seguinte divisão de polinômios usando a regra de Ruffini:
![]()
Neste caso particular o polinômio do dividendo não possui termo de segundo grau, devemos portanto colocar um zero em seu lugar:
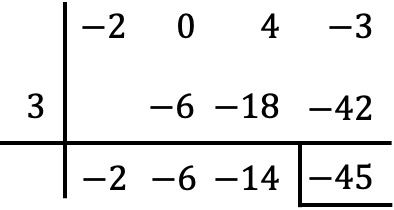
O resultado da divisão entre os 2 polinômios é portanto:
Quociente:
![]()
Descansar:
![]()
Exercício 3
Encontre o resultado da seguinte divisão de polinômios pela regra de Ruffini:
![]()
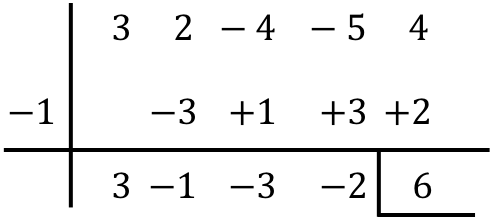
Concluindo, o resultado da divisão dos dois polinômios é:
Quociente:
![]()
Descansar:
![]()
Exercício 4
Encontre o valor da incógnita m de modo que o resto da seguinte divisão dos polinômios seja equivalente a 5:
![]()
Como o divisor tem a forma (xr) ou (x+r), podemos aplicar a regra de Ruffini para resolver a divisão. Portanto, aplicamos o método de Ruffini arrastando a incógnita m:
Agora igualamos o resto obtido a 5, porque o resto deve ser 5:
![]()
E resolvemos a equação para encontrar o valor do parâmetro m :
![]()
![]()
Assim, quando a variável m for equivalente a 3, o resto da divisão entre os polinômios será igual a 5.
Exercício 5
Determine o valor do parâmetro m de modo que o restante da seguinte divisão polinomial dê 3:
![]()
Como o divisor tem a forma (xr) ou (x+r), podemos aplicar a regra de Ruffini para resolver a divisão. Portanto, usamos o método de Ruffini arrastando o desconhecido m:
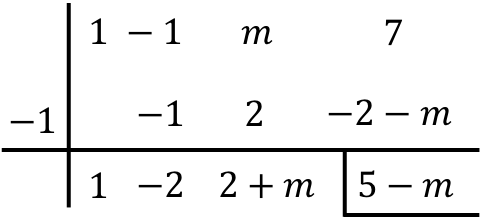
Tenha em mente a propriedade distributiva durante a última multiplicação:
![]()
Por outro lado, o cálculo do restante da divisão é:
![]()
![]()
![]()
Agora igualamos a expressão do resto resultante a 3, uma vez que o resto da divisão deve ser igual a 3:
![]()
E resolvemos a equação resultante para determinar o valor do parâmetro m :
![]()
![]()
![]()
![]()
Portanto, m deve ser igual a 2 para que o restante da divisão polinomial seja igual a 3.
Mais aplicações da regra de Ruffini
Conforme explicado, a regra de Ruffini é usada principalmente para realizar divisão entre polinômios. Porém, a regra de Ruffini também é utilizada para realizar outros cálculos, veremos cada um deles a seguir.
Raízes de um polinômio
As raízes de um polinômio podem ser facilmente determinadas usando a regra de Ruffini. Se você não sabe o que é a raiz de um polinômio, vamos revisar sua definição:
As raízes (ou zeros) de um polinômio são os valores que cancelam o polinômio. Ou seja, as raízes de um polinômio são todos aqueles valores que quando avaliados no polinômio possuem valor numérico igual a 0.
![]()
Por outro lado, sabemos graças ao teorema do resto que se o valor numérico de um polinômio para um determinado valor
![]()
é zero, necessariamente o resto da divisão do referido polinômio entre
![]()
Também deve ser 0.
![]()
Portanto, se você usar a regra de Ruffini para dividir um polinômio
![]()
entre outro polinômio da forma
![]()
obtemos um resto igual a 0, isso significa que
![]()
é uma raiz do polinômio
![]()
Com um exemplo, certamente entenderemos melhor:
- Verifique se
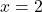
é uma raiz do polinômio
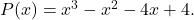
Para verificar se o valor fornecido é raiz do polinômio, basta aplicar o método Ruffini com o referido polinômio e o referido valor:
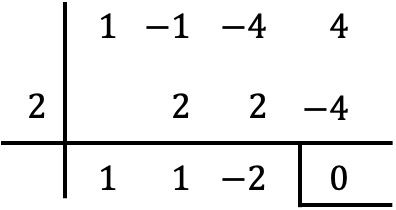
Como o resto obtido pela regra de Ruffini é igual a zero, isso significa que efetivamente
![]()
é uma raiz do polinômio
![]()
Fatoração de polinômios
A regra de Ruffini é o método normalmente aplicado a polinômios fatoriais, pois permite conhecer rapidamente todas as raízes de um polinômio de grau 3, 4, 5, etc.
Então vamos ver como fatorar um polinômio com o algoritmo de Ruffini usando um exemplo:
- Fatore o seguinte polinômio de terceiro grau:
![]()
A primeira coisa a fazer é encontrar todas as raízes do polinômio. E as possíveis raízes de um polinômio são os divisores do termo independente, que neste caso é 6. Então:
Raízes possíveis do polinômio: +1, -1, +2, -2, +3, -3, +6, -6
Precisamos agora tentar dividir o polinômio entre cada um desses valores com a regra de Ruffini. Se o resto da divisão for 0, isso significa que o valor é uma raiz do polinômio; entretanto, se o resto da divisão for diferente de 0, o valor não será uma raiz do polinômio. Assim, testar a regra de Ruffini com todos os números apenas cancela o resto nos três casos seguintes:
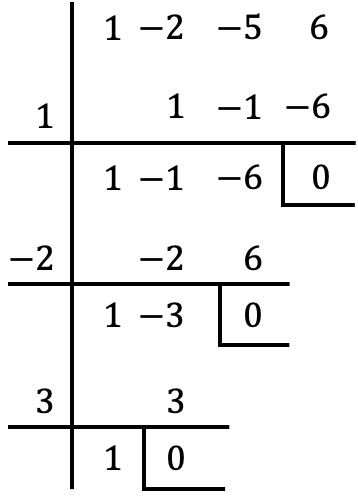
Portanto, as raízes do polinômio no problema são os valores com os quais o resto desaparece, ou seja:
![]()
Finalmente, para fatorar o polinômio devemos expressar cada raiz
![]()
na forma de um fator do tipo
![]()
, ou seja, para cada raiz você deve colocar um parêntese com um
![]()
e a raiz encontrada mudou de sinal:
![]()
Como você pode ver, fatoramos o polinômio com sucesso usando a regra de Ruffini. Porém, você pode ter tido dúvidas sobre fatoração de polinômios por se tratar de um tema muito complexo. Neste caso você pode pesquisar em nosso site (no mecanismo de busca no canto superior direito) o artigo que temos sobre como fatorar polinômios , lá explicamos com mais detalhes e você pode praticar com ele exercícios resolvidos passo a passo. Além disso, também mostramos outros métodos para fatorar polinômios.
Calcule o valor numérico de um polinômio
Embora possa parecer surpreendente, o valor numérico de um polinômio pode ser determinado pela regra de Ruffini usando o teorema do resto.
Mas obviamente, para fazer isso você precisa conhecer o teorema do resto. Caso contrário, você pode procurar a explicação do teorema do resto em nosso site (no mecanismo de busca no canto superior direito) .
Assim, graças ao teorema do resto, podemos saber o valor numérico de qualquer polinômio. Vamos ver como fazer isso usando um exemplo:
- Calcule o valor numérico de

Para
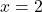
aplicando a regra de Ruffini, sendo
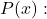
![]()
Para encontrar o valor numérico do polinômio para o valor
![]()
A única coisa que precisamos fazer é usar a regra de Ruffini com o polinômio e o referido valor:
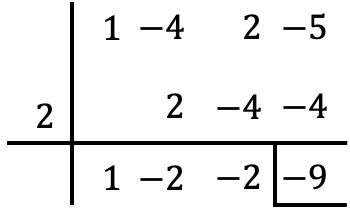
Assim, pelo teorema do resto, sabemos que o valor numérico do polinômio coincide com o resto da divisão polinomial . Portanto, o valor numérico do polinômio em
![]()
é -9.
![]()
Por outro lado, podemos verificar que a regra de Ruffini é aplicada corretamente calculando numericamente o valor numérico:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Resolva equações de terceiro grau ou superior
Outra aplicação da regra de Ruffini é resolver equações de grau maior que 2, pois nestes casos não existe fórmula como na equação de segundo grau. Vamos ver como fazer isso usando um exemplo:
- Resolva a seguinte equação quadrática usando a regra de Ruffini:
![]()
Precisamos tratar a equação como se fosse um polinômio. Então, devemos calcular tantas raízes do “polinômio” usando a regra de Ruffini até obtermos uma equação de segundo grau . Neste caso é uma equação de grau 3, portanto é suficiente determinar uma raiz do “polinômio”:
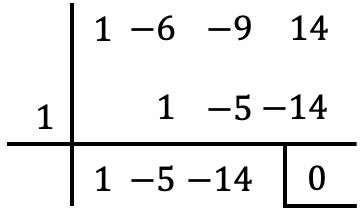
Uma solução da equação será, portanto,
![]()
Pois bem, para encontrar as demais soluções, devemos colocar o polinômio obtido no quociente da regra de Ruffini igual a 0:
![]()
E agora resolvemos a equação quadrática resultante com sua fórmula correspondente:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
Concluindo, as 3 soluções da equação do terceiro grau são:
![]()