Neste artigo explicamos como derivar o arco tangente hiperbólico de uma função. Além disso, você poderá ver exemplos resolvidos da derivada da arcotangente hiperbólica.
Fórmula para a derivada da arcotangente hiperbólica
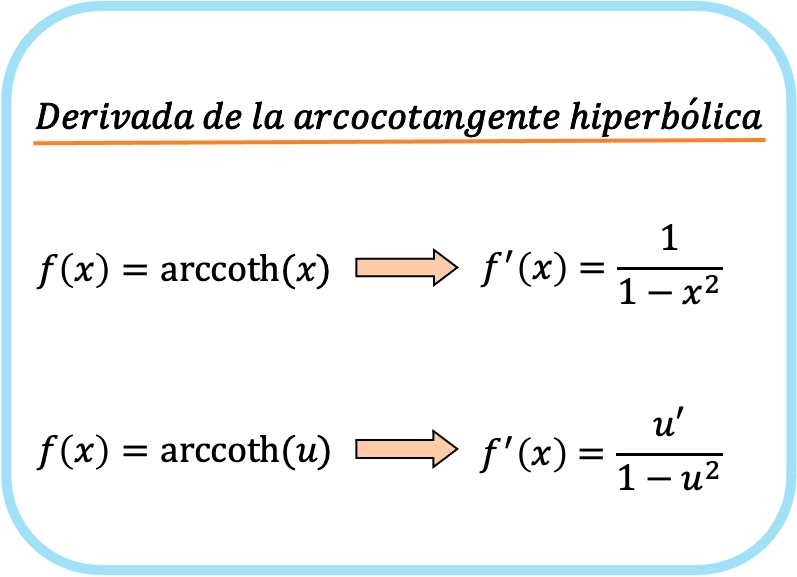
A derivada do arco tangente hiperbólico de x é um sobre um menos x ao quadrado.
![]()
Portanto, a derivada do arco tangente hiperbólico de uma função é igual ao quociente da derivada dessa função dividido por um menos essa função ao quadrado.
![]()
Observe que a segunda fórmula é semelhante à primeira, mas aplica a regra da cadeia, portanto, elas podem ser consideradas a mesma fórmula.
Você pode ver em alguns livros de matemática que a derivada deste tipo de função trigonométrica inversa é:
![]()
Porém, se você olhar com atenção, são a mesma fórmula, a única diferença é que o numerador e o denominador da fração foram multiplicados por -1.
Exemplos de derivada da arcotangente hiperbólica
Exemplo 1
![]()
No argumento arcotangente hiperbólico temos uma função diferente de x, então precisamos usar a fórmula da regra da cadeia para derivá-la:
![]()
A derivada de 5x é 5, então coloque 5 no numerador da fração e coloque menos 5x ao quadrado no denominador:
![]()
Exemplo 2
![]()
Para resolver a derivada desta função, precisamos aplicar a fórmula da derivada da arcotangente hiperbólica, que é a seguinte:
![]()
Neste caso temos uma função composta, pois existe uma função exponencial no argumento da função trigonométrica. Portanto, precisamos usar a regra da cadeia para encontrar a derivada de toda a função:
![]()