Derivada da cotangente hiperbólica

Aqui explicamos como derivar a cotangente hiperbólica de uma função. Você também encontrará exemplos da derivada da cotangente hiperbólica.

Fórmula para a derivada da cotangente hiperbólica

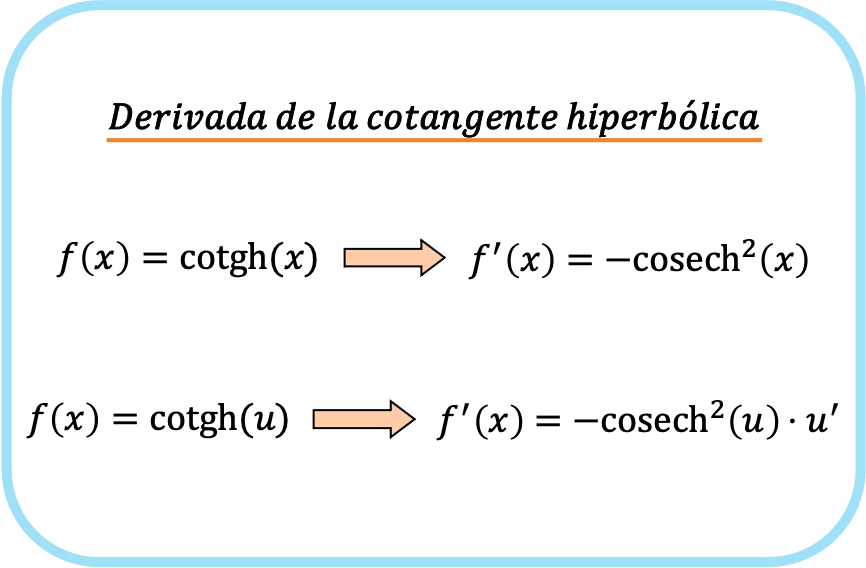
A derivada da cotangente hiperbólica de x é igual a menos a cossecante hiperbólica de x ao quadrado.

f(x)=\text{cotgh}(x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(x)

Portanto, a derivada da cotangente hiperbólica de uma função é menos a cossecante hiperbólica da função vezes a derivada dessa função.

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Tenha em mente que na segunda fórmula foi aplicada a regra da cadeia e esta fórmula é usada quando há uma função diferente de x no argumento da cotangente hiperbólica.

derivado da cotangente hiperbólica

Você pode encontrar em alguns livros de matemática que a derivada da cotangente é outra, já que as três expressões a seguir são equivalentes:

f'(x)=-\text{cosech}^2(x)=1-\text{cotgh}^2(x)=-\cfrac{1}{\text{senh}^2(x)}

Obviamente, você pode usar qualquer expressão que preferir entre as três para derivar a cotangente hiperbólica, mas a mais usada é a cossecante hiperbólica ao quadrado.

Exemplos de derivada da cotangente hiperbólica

Depois de sabermos qual é a fórmula da derivada da cotangente hiperbólica de uma função, resolveremos vários exemplos deste tipo de derivadas trigonométricas.

Exemplo 1

Neste exemplo veremos qual é a derivada da cotangente hiperbólica da função 2x.

f(x)=\text{cotgh}(2x)

No argumento da cotangente hiperbólica temos uma função diferente de x, então precisamos usar a fórmula com a regra da cadeia para fazer a derivação:

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Como 2x é um termo de primeiro grau, sua derivada é 2. Portanto, para encontrar a derivada da cotangente hiperbólica de 2x, simplesmente colocamos 2x no argumento ao quadrado da cossecante hiperbólica e multiplicamos por 2.

f(x)=\text{cotgh}(2x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(2x)\cdot 2

Exemplo 2

No segundo exemplo, determinaremos o valor da derivada da cotangente hiperbólica de uma função polinomial.

f(x)=\text{cotgh}(3x^4-5x)

Como vimos acima, a regra para derivar a cotangente hiperbólica de uma função é a seguinte:

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Portanto, a derivada da cotangente hiperbólica deste exercício será a seguinte:

f(x)=\text{cotgh}(3x^4-5x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(3x^4-5x)\cdot(12x^3-5)

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima