Derivada secante hiperbólica

Neste artigo explicamos como derivar a secante hiperbólica de uma função. Você encontrará a fórmula da derivada da secante hiperbólica e vários exemplos trabalhados deste tipo de derivada.

Fórmula para a derivada da secante hiperbólica

A derivada da secante hiperbólica de x é igual a menos o produto da secante hiperbólica de x vezes a tangente hiperbólica de x.

f(x)=\text{sech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x)\cdot \text{tanh}(x)

Portanto, a derivada da secante hiperbólica de uma função é menos o produto da secante hiperbólica da função vezes a tangente hiperbólica da função vezes a derivada da referida função.

f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'

Resumindo, a fórmula para a derivada da função secante hiperbólica é:

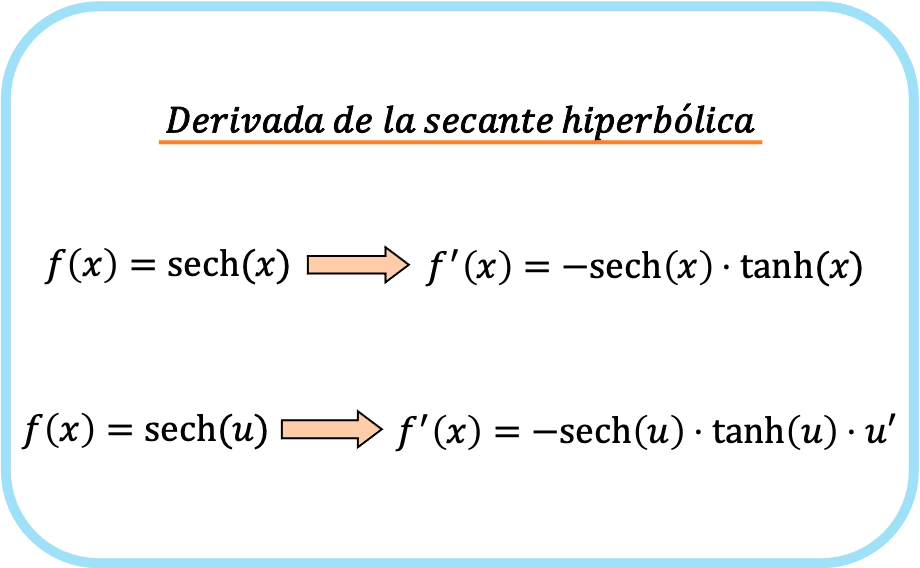
derivado da secante hiperbólica

Observe que ambas as expressões pertencem, na verdade, a uma única fórmula. A única diferença é que na segunda fórmula é aplicada a regra da cadeia.

Exemplos de derivada da secante hiperbólica

Agora que conhecemos a fórmula da derivada da secante hiperbólica, veremos vários exercícios resolvidos deste tipo de derivada trigonométrica.

Exemplo 1

f(x)=\text{sech}(2x)

Neste exemplo, temos uma função diferente de x no argumento da secante hiperbólica, portanto, para derivá-la, precisamos usar a fórmula da regra da cadeia.

f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'

Como a função 2x é linear, sua derivada é 2. Portanto, para encontrar a derivada, simplesmente substituímos u por 2x e u’ por 2 na fórmula:

f(x)=\text{sech}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(2x)\cdot \text{tanh}(2x)\cdot 2

Exemplo 2

f(x)=\text{sech}(x^2)

A função deste exercício é composta, pois a secante hiperbólica tem outra função no seu argumento. Devemos, portanto, usar a fórmula da secante hiperbólica com a regra da cadeia para fazer sua derivação:

f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'

A derivada de x elevada a 2 dá 2x, então a derivada da secante hiperbólica de x ao quadrado é:

f(x)=\text{sech}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x^2)\cdot \text{tanh}(x^2)\cdot 2x

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima