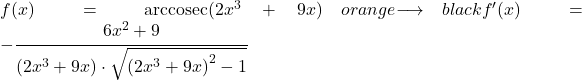Nesta página você verá qual é a fórmula da derivada do arcossecante. Além disso, você poderá ver exercícios resolvidos para derivadas do arco cossecante de uma função.
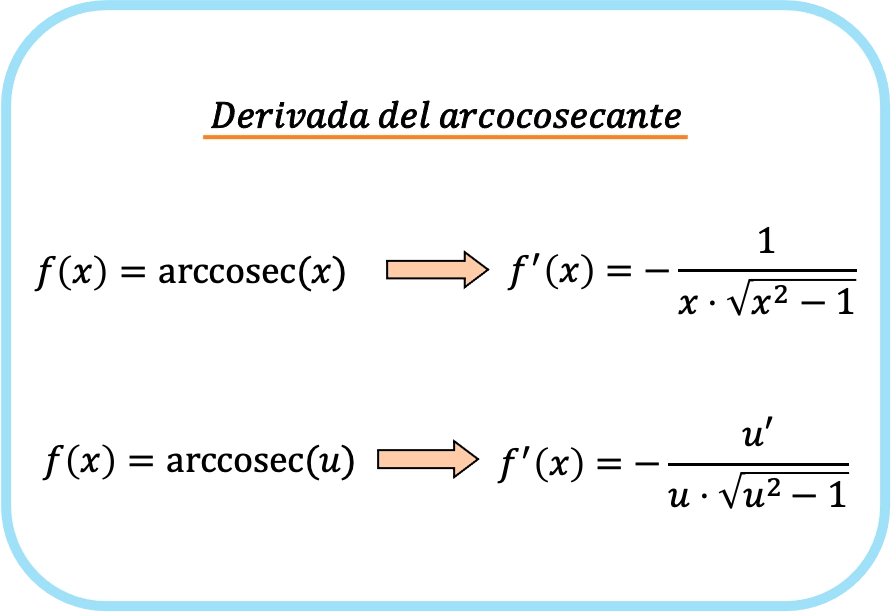
Fórmula derivada de arcossecante
A derivada do arco-secante de x é menos um sobre o produto de x vezes a raiz de x ao quadrado menos 1.
![]()
Portanto, a derivada do arco-secante de uma função é igual a menos o quociente da derivada dessa função dividida pela função vezes a raiz dessa função ao quadrado menos um.
![]()
Na verdade, as duas fórmulas anteriores são iguais, mas na segunda expressão é aplicada a regra da cadeia. Na verdade, se você substituir a função identidade x em u, obterá a derivada do arcossecante de x, já que a derivada de x é um.
Como você bem sabe, a arcossecante é a função trigonométrica inversa da cossecante, porém suas derivadas são bem diferentes. Você pode ver a fórmula para este outro tipo de função trigonométrica no seguinte link:
➤ Veja: derivada da cossecante
Exemplos de derivada do arco cossecante
Vendo o que é a regra da derivada arcossecante, resolveremos a seguir dois exemplos deste tipo de derivada. Mas se você ainda tiver alguma dúvida sobre como derivar o arco cossecante, pode nos perguntar nos comentários.
Exemplo 1
Neste exemplo, veremos quanto é a derivada do arco cossecante da função quadrática x 2 .
![]()
Para calcular a derivada do arco secante de x ao quadrado, aplicamos a fórmula que vimos acima:
![]()
A derivada de x elevado a dois é 2x, então a derivada da função composta é:
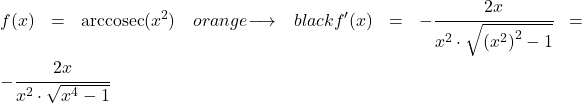
Exemplo 2
Neste segundo exemplo, derivaremos o arco-secante de uma função potencial.
![]()
Precisamos de utilizar a regra da derivada do arco secante para determinar a derivada de toda a função.
![]()
Assim, no numerador escrevemos a derivada do argumento da função, e no denominador reescrevemos a função potencial e multiplicamos pela raiz quadrada da função do argumento ao quadrado menos 1: