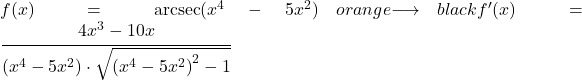Nesta página você verá qual é a derivada do arco secante (fórmula). Você encontrará exercícios resolvidos para derivadas do arco secante de uma função.
Fórmula derivada do arco secante
A derivada do arco secante de x é um sobre o produto de x vezes a raiz de x ao quadrado menos 1.
![]()
Portanto, a derivada do arco secante de uma função é igual ao quociente da derivada dessa função dividida pela função vezes a raiz dessa função ao quadrado menos um.
![]()
Obviamente, a segunda fórmula é semelhante à primeira fórmula, a única diferença entre as duas é que a regra da cadeia é aplicada na segunda fórmula.

Embora possa parecer estranho por serem funções inversas, a derivada do arco secante nada tem a ver com a derivada da secante. Você pode ver a fórmula da derivada da secante clicando aqui:
➤ Veja: derivada da secante
Exemplos de derivada de arco secante
Exemplo 1
Neste exemplo, veremos quanto é a derivada do arco secante da função linear 7x.
![]()
Para encontrar a derivada do arco secante você deve aplicar sua fórmula correspondente, que é a seguinte:
![]()
A derivada da função 7x é 7, então a derivada do arco secante da função 7x é:
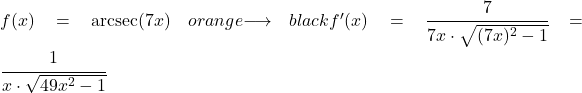
Exemplo 2
Neste segundo exemplo, derivaremos o arco secante de uma função potencial.
![]()
Como existe um termo diferente de x no argumento da função arco-secante, precisamos aplicar a regra da derivada do arco-secante com a regra da cadeia para derivar a função inteira.
![]()
Assim, no numerador escrevemos a derivada do argumento da função, e no denominador reescrevemos a função potencial e multiplicamos pela raiz quadrada da função do argumento elevada à potência de 2 menos 1: