Neste artigo explicamos como derivar a cossecante de uma função (fórmula). Você também encontrará exercícios resolvidos passo a passo para a derivada da cossecante. E por fim, você poderá ver a demonstração da fórmula desse tipo de derivada trigonométrica.
Fórmula derivada cossecante
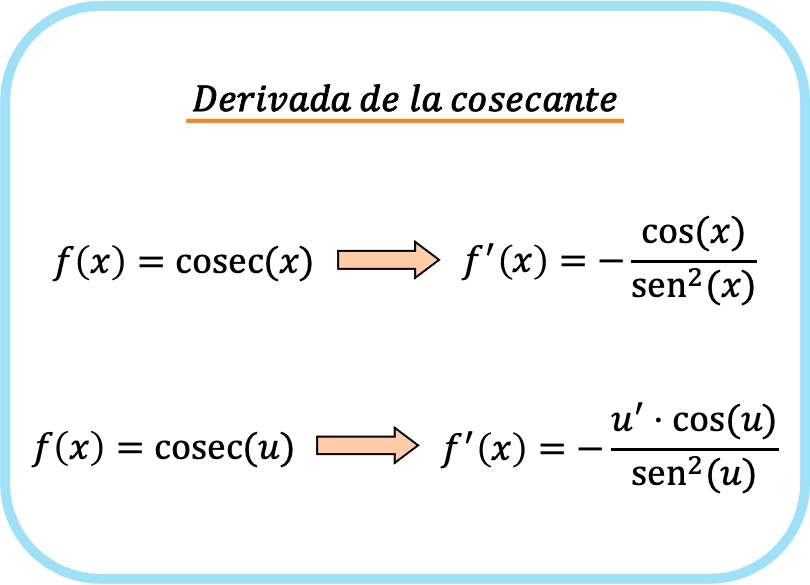
A derivada da cossecante de x é igual a menos o quociente do cosseno de x dividido pelo seno quadrado de x.
![]()
Usando fórmulas trigonométricas, também podemos definir a derivada da cossecante de x como menos o produto da cotangente de x vezes a cossecante de x.
![]()
E se aplicarmos a regra da cadeia, a derivada da cossecante de uma função é menos o produto da derivada da função vezes o cosseno da função, dividido pelo seno ao quadrado da função.
![]()
A fórmula usada para derivar a cossecante de uma função é, portanto, a seguinte:
Exemplos de derivada da cossecante
Tendo visto qual é a fórmula da derivada da cossecante, daremos agora vários exemplos. Assim você pode ver exatamente como a cossecante de uma função é derivada.
Exemplo 1: Derivada da cossecante de 2x
Neste exemplo veremos quanto é a derivada da cossecante de 2x:
![]()
A função do argumento da cossecante é diferente de x, então precisamos usar a regra da derivada da cossecante com a regra da cadeia.
![]()
Então, para encontrar a derivada dessa função trigonométrica, basta substituir os valores da fórmula anterior: no argumento cosseno e seno colocamos 2x, e u’ corresponde à derivada de 2x, ou seja, 2:
![]()
Exemplo 2: Derivada da cossecante de x ao quadrado
Neste exercício, veremos quanto é a derivada da cossecante de x ao quadrado:
![]()
Logicamente, a derivada desta função trigonométrica é resolvida usando a fórmula da derivada da cossecante:
![]()
A derivada de x ao quadrado dá 2x, então a derivada da cossecante de x elevada a dois é:
![]()
Exemplo 3: Derivada da cossecante ao cubo de uma função exponencial
![]()
Qualquer que seja o argumento da função, a regra para a derivada da cossecante de uma função é:
![]()
Mas neste caso temos uma função composta, porque a cossecante é elevada a três e, além disso, no seu argumento há uma função exponencial. Então, para derivar toda a função, precisamos aplicar a regra da cadeia várias vezes:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ac2ce49dfcba1b7f27696dba0a2decb_l3.png)
Problemas resolvidos da derivada da cossecante
Derive as seguintes funções cossecantes:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32dde68d2a11ef6a05d483b26f0a98ef_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bea25dae467cefdcc1bd48e8d9bc88_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb70e1d7b6f2ce2636934b235904861f_l3.png)
Prova da fórmula da derivada da cossecante
A seguir, demonstraremos a fórmula da derivada da cossecante. Ao contrário de outras demonstrações, neste caso não utilizaremos o limite que define uma derivada, mas partiremos da definição matemática da cossecante.
Algebricamente, a função trigonométrica cossecante é o inverso multiplicativo do seno:
![]()
Podemos, portanto, derivar a cossecante usando a regra do quociente:
![]()
![]()
Como você pode ver, é somente aplicando a regra da derivada de uma divisão que chegamos à fórmula da derivada da cossecante. E como a derivada de um quociente já está provada (você pode ver no link a seguir), a regra da derivada da cossecante também está provada.