Aqui explicamos como derivar o arco cosseno de uma função. Além disso, você encontrará exemplos de derivadas do arco cosseno e poderá praticar com exercícios resolvidos passo a passo. Finalmente, mostramos a prova da fórmula da derivada do arco cosseno.
Qual é a derivada do arco cosseno?
A derivada do arco cosseno de x é menos um sobre a raiz quadrada de um menos x ao quadrado.
![]()
Portanto, a derivada do arco cosseno de uma função é igual a menos o quociente da derivada dessa função dividido pela raiz quadrada de um menos essa função ao quadrado.
![]()
Na verdade, a primeira fórmula é obtida substituindo x por u na segunda fórmula. Então, para recapitular, a fórmula para a derivada do cosseno inverso é:

Como você pode ver, a fórmula da derivada do arco cosseno é como aderivada do arco seno , mas adicionando um negativo antes dela.
Exemplos da derivada do arco cosseno
Dada a fórmula da derivada da função arcocosseno, analisaremos agora vários exemplos deste tipo de derivadas trigonométricas. Dessa forma, será mais fácil entender como o arco cosseno de uma função é derivado.
Exemplo 1: Derivada do arco cosseno de 2x
![]()
Para resolver a derivada do arco cosseno, usamos sua fórmula:
![]()
A derivada de 2x é 2, então a derivada do arco cosseno de 2x é menos 2 sobre a raiz de um menos 2x ao quadrado:
![]()
Exemplo 2: Derivada do arco cosseno de x ao quadrado
![]()
Aplicamos a fórmula da derivada do arco cosseno com a regra da cadeia para calcular a derivada:
![]()
Como a derivada da função x 2 é 2x, a derivada do arco cosseno de x elevado a 2 é:
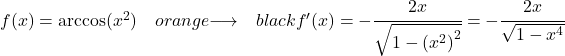
Exemplo 3: Derivada do arco cosseno de um logaritmo
![]()
A função neste exemplo é uma função composta por um arco cosseno e um logaritmo natural, por isso precisamos de utilizar a regra da cadeia para derivá-la.
![]()
A derivada do logaritmo natural é dividida por x, portanto a derivada da função inteira é:
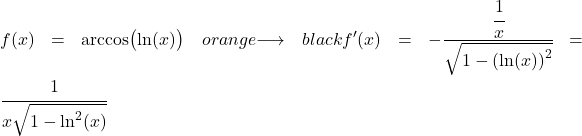
Derivada de arcoseno resolveu problemas
Derive as seguintes funções arcosseno:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ffd255c55afc3967dc250bc63741575_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec25311613f0552bbc52d2d15581d3fb_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1a362c38a56084dec3c6ebbccba9ab0_l3.png)
Prova da fórmula da derivada do arco cosseno
Nesta seção, demonstraremos a fórmula da derivada do arco cosseno.
![]()
Primeiro, transformamos o arco cosseno em cosseno:
![]()
Deduzimos agora os dois lados da igualdade:
![]()
Nós limpamos você:
![]()
Usamos a identidade trigonométrica fundamental para transformar seno em cosseno:
![]()
![]()
Mas acima deduzimos que x é igual ao cosseno de y, então a equação permanece:
![]()
E assim chegamos à expressão para a derivada do arco cosseno, então sua fórmula está demonstrada.