Derivado de uma raiz

Aqui explicamos como derivar uma raiz (ou uma função radical). Você encontrará a fórmula de divisão de raízes e exercícios resolvidos passo a passo para derivadas de raízes.

Fórmula para a derivada de uma raiz

A derivada de uma raiz, ou função irracional, é igual à derivada do radicando (expressão abaixo do radical) dividida pelo produto do índice da raiz vezes a mesma raiz, subtraindo 1 do expoente do radicando.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

No entanto, se o radicando raiz for apenas um x, as fórmulas serão simplificadas. A derivada raiz de x é, portanto, a seguinte:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Resumindo, existem duas fórmulas para derivar uma raiz: a primeira que sempre pode ser usada e a segunda que só pode ser usada quando o radicando for x.

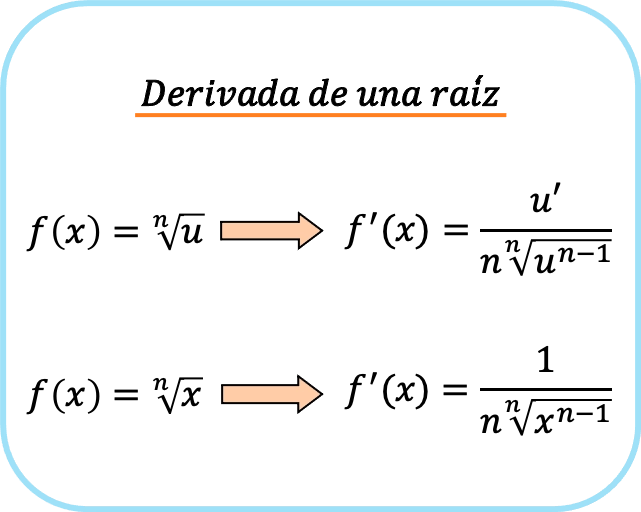
Se você olhar de perto, o termo no numerador da fração é aquele que resulta da aplicação da regra da cadeia ao calcular a derivada da raiz. É por isso que quando o radicando é x, 1 aparece no denominador, pois é a derivada de x.

Exemplos de derivadas de raiz

Dada a fórmula da derivada de uma função radical, explicamos a seguir vários exemplos desse tipo de derivada para que você entenda como derivar uma raiz.

Exemplo 1: Derivada de uma raiz quadrada

Veremos então qual é a derivada de uma raiz quadrada:

$f(x)=\sqrt{x}$

Neste caso, a expressão dentro da raiz é apenas um x, então podemos usar a seguinte fórmula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Portanto, a derivada de uma raiz quadrada é igual a 1 dividido pelo produto de 2 vezes a raiz quadrada de x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Exemplo 2: Derivada de uma raiz cúbica

$f(x)=\sqrt[3]{x}$

Neste exemplo, a expressão sob a raiz é x, então podemos aplicar a seguinte fórmula:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Portanto, a derivada de uma raiz cúbica é igual a 1 dividido por 3 vezes a raiz cúbica de x ao quadrado:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Exemplo 3: Derivada de uma raiz quarta

$f(x)=\sqrt[4]{7x-2}$

Agora não temos x sob o sinal radical, mas temos uma expressão algébrica mais complexa. Portanto, devemos usar a fórmula geral para a derivada de uma raiz:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

A expressão sob o radical é uma função de primeiro grau, então sua derivada é 7. Assim, a derivada de toda a função é:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Exemplo 4: Derivação de uma raiz para outra

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Para resolver a derivada desta raiz composta por outra raiz, devemos aplicar a seguinte fórmula:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Neste caso, você deve usar a mesma fórmula duas vezes seguidas para calcular a derivada:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Problemas resolvidos da derivada de uma raiz

Calcule as derivadas das seguintes raízes:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

veja solução

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Fórmula para a derivada de uma raiz

Exemplos de derivadas de raiz

Exemplo 1: Derivada de uma raiz quadrada

Exemplo 2: Derivada de uma raiz cúbica

Exemplo 3: Derivada de uma raiz quarta

Exemplo 4: Derivação de uma raiz para outra

Problemas resolvidos da derivada de uma raiz

Deixe um comentário Cancelar resposta