Neste artigo mostramos quanto é a derivada de uma função linear. Adicionalmente, resolvemos vários exemplos de derivadas de funções lineares e demonstramos a fórmula para este tipo de derivada. Você encontrará até exercícios resolvidos sobre derivadas de funções lineares.
Qual é a derivada de uma função linear?
A derivada de uma função linear é o coeficiente do termo de primeiro grau , ou seja, a derivada de uma função linear f(x)=Ax+B é igual a A.
![]()
O termo independente é removido da derivada porque a derivada de uma constante é zero. E, por outro lado, a derivada de um termo de primeiro grau é o coeficiente desse termo. Portanto, a derivada da soma desses dois tipos de funções é o coeficiente do termo linear.
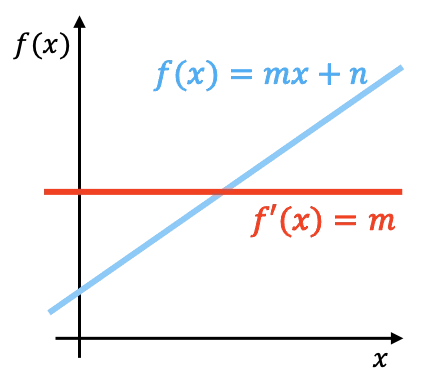
Geometricamente, a derivada de uma função linear é a inclinação dessa função. No gráfico acima você pode ver representada uma função linear com sua derivada.
Exemplos de derivadas de funções lineares
Dada a definição da derivada de uma função linear, calcularemos vários exemplos de funções lineares para finalizar a compreensão do conceito:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b12cfa0a6432f8171149ec0139d259ce_l3.png)
Lembre-se que a derivada da função linear é sempre o número que acompanha a variável x quando a função não possui termo independente, ou seja, se possui apenas um termo de primeiro grau. Por exemplo:
![]()
Portanto, a derivada de uma função linear é uma função sem variável independente, um número simples.
Prova da derivada de uma função linear
A seguir, demonstraremos a fórmula da derivada de uma função linear.
Seja f qualquer função linear:
![]()
A fórmula para calcular a derivada de uma função em um ponto é:
![]()
Então, se calcularmos o limite anterior para uma função linear, obtemos:
![]()
Resolvemos os parênteses:
![]()
Operamos no numerador:
![]()
E finalmente, simplificamos a fração:
![]()
Concluindo, a derivada de uma função linear é igual ao coeficiente do termo de primeiro grau em qualquer ponto. Assim, a fórmula para a derivada de uma função linear é derivada.
Problemas resolvidos de derivadas de funções lineares
Calcule as derivadas das seguintes funções lineares:
![]()
![]()
![]()
![]()
![]()
![]()
Para derivar uma função linear, basta eliminar o termo constante e a variável da função, de modo que permaneça apenas o coeficiente do termo linear. Ainda:
![]()
![]()
![]()
![]()
![]()
![]()
Embora os coeficientes da função sejam frações ou raízes, a derivação da função linear é feita da mesma forma.