Neste artigo explicamos como calcular o infinito da indeterminação entre o infinito (∞/∞). Você encontrará exemplos desta indeterminação com todos os tipos de funções: funções polinomiais, radicais, exponenciais, etc. Além disso, você poderá treinar com exercícios resolvidos passo a passo de limites que dão infinitas indeterminações entre infinitos.
Como resolver a indeterminação infinita entre infinito
Quando o limite de uma função dá infinito dividido por infinito, significa que se trata de uma indeterminação (ou forma indeterminada). Para resolver o limite de uma função que dá infinito de indeterminação entre o infinito, o grau do polinômio do numerador deve ser comparado ao grau do polinômio do denominador.
![]()
O resultado da indeterminação infinito dividido pelo infinito depende do grau do numerador e do grau do denominador da fração:
- Se o grau do polinômio do numerador for menor que o grau do polinômio do denominador, o infinito da indeterminação dividido pelo infinito é igual a zero.
- Se o grau do polinômio do numerador for equivalente ao grau do polinômio do denominador, a indeterminação infinita sobre o infinito é o quociente dos coeficientes principais dos dois polinômios.
- Se o grau do polinômio do numerador for maior que o grau do polinômio do denominador, o infinito da indeterminação entre o infinito dá mais ou menos infinito (o sinal depende dos termos principais dos dois polinômios).
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
<h2 class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png) Exemplos de indeterminações infinitas entre o infinito
Exemplos de indeterminações infinitas entre o infinito
Vamos ver como a forma indeterminada infinito entre infinito é resolvida observando vários exemplos de cada caso:
grau do numerador menor que o grau do denominador
Como vimos acima, quando o grau do polinômio do numerador é menor que o grau do polinômio do denominador, o limite infinito indeterminado entre o infinito sempre dá 0.
Exemplo 1:
![]()
O polinômio do numerador é de segundo grau, enquanto o do denominador é de terceiro grau, então a solução do limite é 0.
Exemplo 2:
![]()
A função polinomial do numerador é de primeiro grau, mas a função do denominador é de quarto grau, então o limite ao infinito negativo é 0.
grau do numerador igual ao grau do denominador
Quando o grau do polinômio do numerador é igual ao grau do polinômio do denominador, o limite indeterminado infinito por infinito é calculado dividindo os coeficientes líderes (coeficiente do termo de grau superior) dos dois polinômios.
Exemplo 3:
![]()
Neste caso, os dois polinômios são de segundo grau, portanto é necessário dividir os coeficientes dos termos de grau superior para encontrar o limite no infinito positivo.
Exemplo 4:
![]()
Embora o limite seja quando x tende a menos infinito, a indeterminação infinita entre o infinito se resolve da mesma maneira.
Grau do numerador maior que o grau do denominador
Quando o grau do polinômio do numerador é maior que o grau do polinômio do denominador, a forma indeterminada do infinito entre o infinito sempre dará o infinito, e o sinal do infinito é determinado pelos termos de grau superior dos dois polinômios.
Exemplo 5:
![]()
A função do numerador tem um grau superior ao do denominador, então a indeterminação infinito sobre infinito dá infinito. Além disso, neste caso tanto o numerador quanto o denominador obtêm infinito positivo, então o resultado do limite também deve ser positivo.
Exemplo 6:
![]()
Neste problema, um infinito positivo é obtido do numerador porque qualquer termo quadrado é positivo, por outro lado, um infinito negativo é obtido do denominador. Portanto, o limite resultante é negativo porque positivo dividido por negativo é igual a negativo.
Indeterminação infinita entre o infinito com raízes
Acabamos de ver como calcular a indeterminação infinita entre o infinito quando temos funções polinomiais. Mas… quanto é o infinito dividido pelo infinito se tivermos raízes?
O grau de uma função irracional (função com raízes) é o quociente entre o grau do termo principal e o índice do radical.
![Rendered by QuickLaTeX.com \sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffc00917d2cc316211a57feafdddd0d2_l3.png)
Portanto, se o limite de uma função com raízes dá a indeterminação entre o infinito , devemos aplicar as mesmas regras explicadas acima para os graus do numerador e do denominador, mas levando em consideração que o grau de um polinômio com raízes é calculado de forma diferente.
Veja o seguinte exemplo do limite ao infinito de uma função com radicais:
![]()
O grau do numerador é 2 e o grau do denominador é 4 (8/2=4), portanto o limite é 0 porque o grau do numerador é menor que o grau do denominador.
Por outro lado, se o grau do numerador e do denominador forem iguais, para calcular o limite indeterminado devemos tomar o coeficiente principal com o radical:
![]()
Indeterminação infinita entre o infinito com funções exponenciais
Por fim, só nos resta estudar um caso de quociente de indeterminação de infinitos: quanto é a indeterminação infinita entre infinito e funções exponenciais.
O crescimento de uma função exponencial é muito maior que o crescimento de uma função polinomial, portanto devemos considerar que o grau de uma função exponencial é maior que o grau de uma função polinomial.
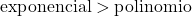
![]()
Neste caso, o denominador é formado por uma função exponencial, portanto é de ordem superior ao numerador. Portanto, a forma indeterminada infinito entre o infinito desaparece.
Exercícios resolvidos de indeterminação infinita entre o infinito
Exercício 1
Calcule o limite da seguinte função racional:
![]()
Ao calcular o limite, obtemos a indeterminação infinita entre o infinito, mas como o grau do numerador é menor que o grau do denominador, o limite indeterminado é igual a zero.
![]()
Exercício 2
Resolva o seguinte limite indeterminado:
![]()
Ao tentar calcular o limite, obtém-se a indeterminação ∞/∞. Neste caso, o grau do polinômio do numerador é maior que o grau do polinômio do denominador, portanto o limite indeterminado é igual a mais infinito.
![]()
Exercício 3
Resolva o seguinte limite no infinito:
![]()
O limite dá indeterminação menos infinito entre mais infinito. O grau do numerador é maior que o grau do denominador, então o limite indeterminado é igual a mais infinito. Porém, como a divisão é infinito negativo por infinito positivo, o resultado é menos infinito.
![]()
Exercício 4
Resolva o seguinte limite indeterminado:
![]()
Neste problema, a forma infinita indeterminada sobre o infinito é obtida a partir do quociente de dois polinômios de mesmo grau, portanto, o resultado do limite indeterminado é a divisão de seus coeficientes principais:
![]()
Exercício 5
Calcule o seguinte limite pelo menos até o infinito:
![]()
O grau da expressão algébrica do numerador é menor que o grau da expressão do denominador, então a indeterminação +∞/+∞ dá 0:
![]()
Exercício 6
Resolva o seguinte limite indeterminado de uma função com raízes:
![]()
A expressão para o numerador está sob um radical, então seu grau é 7/3. Por outro lado, o polinômio no denominador é quadrático. E como 7/3>2, o limite dá mais infinito:
![]()
Exercício 7
Determine o limite ao infinito da seguinte função com frações:
![]()
Neste exercício, a indeterminação menos infinito dividido por menos infinito é obtida com o grau do numerador maior que o grau do denominador, portanto:
![]()
Exercício 8
Encontre o limite pelo menos ao infinito da seguinte função:
![]()
O polinômio denominador é quadrático, enquanto o polinômio numerador é linear. Portanto, o infinito da indeterminação dividido pelo infinito dá 0.
![]()
Exercício 9
Resolva o limite pelo menos infinito da seguinte função:
![]()
O numerador é de grau maior que o denominador, então o resultado da forma indeterminada ∞/∞ será infinito. Além disso, o sinal do infinito será negativo porque o positivo dividido pelo negativo dá o negativo:
![]()
Exercício 10
Resolva o seguinte limite com indeterminação infinita entre o infinito:
![]()
A função exponencial é de ordem superior à função polinomial, então o limite dará infinito. Porém, dividindo o positivo pelo negativo, o sinal do infinito será negativo:
![]()
Exercício 11
Calcule o seguinte limite:
![]()
Neste problema, a indeterminação infinito no infinito é resolvida dividindo os coeficientes dominantes dos dois polinômios, uma vez que são do mesmo grau:
![]()
Exercício 12
Resolva o limite da seguinte função quando x se aproxima do infinito:
![]()
Embora a incógnita no numerador não seja diretamente elevada ao quadrado, ao resolver a identidade notável podemos ver claramente que o grau do numerador é maior que o grau do denominador. Ainda:
![]()
Exercício 13
Calcule o limite ao infinito da seguinte função com raiz cúbica:
![]()
O numerador é formado por uma raiz cúbica, então seu grau é 3/3=1. Então, o grau do numerador é igual ao do denominador, então a indeterminação infinita entre o infinito é resolvida da seguinte forma:
![]()
Exercício 14
Resolva o limite ao infinito da seguinte função com dois radicais:
![]()
O grau do numerador é 7/3 = 2,33 e o grau do denominador é 5/2 = 2,5. Portanto, como o grau do numerador é menor que o grau do denominador, o limite infinito indeterminado entre o infinito é 0:
![Rendered by QuickLaTeX.com \displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-681401701d7d7f3fad1879db26659942_l3.png)
Exercício 15
Calcule o seguinte limite:
![]()
Independentemente do grau do numerador, como temos uma função exponencial no denominador, o resultado da forma indeterminada infinito sobre infinito é 0:
![]()