Aqui você descobrirá o que é a função identidade. Além disso, você poderá ver como representar graficamente a função identidade e quais são suas características.
O que é uma função de identidade?
Uma função identidade é aquela função que tem como imagem o mesmo valor do argumento. A função identidade pode ser expressa com o termo id .
Portanto, a expressão matemática para a função identidade é:
![]()
Por exemplo, a imagem da função identidade para x=1 vale 1, a imagem de x=2 vale 2, a imagem de x=3 vale 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
A função identidade é um exemplo de função linear. No link a seguir você pode ver mais exemplos deste tipo de funções:
➤ Veja: exemplos de funções lineares
Representação gráfica da função identidade
O gráfico da função identidade corresponde a uma reta que é a bissetriz do primeiro e terceiro quadrantes.
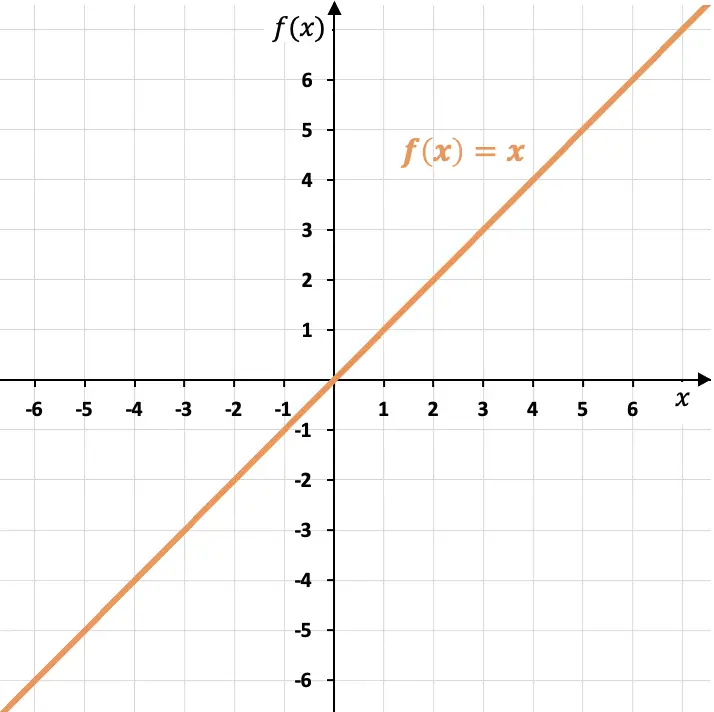
Como você pode ver, a função identidade passa pela origem das coordenadas (ponto (0,0)) e tem inclinação igual à unidade (m=1), pois uma unidade da variável aumenta e para cada valor do independente variável X. Além disso, a função identidade forma um ângulo de 45º com o eixo X.
Características da função identidade
A função identidade possui as seguintes propriedades:
- O domínio da função identidade são todos os números reais:
![]()
- O contradomínio (ou contradomínio) da função identidade também consiste em todos os números reais:
![]()
- A função identidade é uma função contínua e bijetiva.
- Além disso, a função identidade consiste em uma função ímpar, o que significa que é uma função simétrica em relação à origem das coordenadas.
![]()
➤ Veja: função simétrica ímpar
- A função identidade é crescente em todo o seu domínio e sua inclinação é igual a 1.
![]()
- Intersecta o eixo x (eixo OX) e o eixo y (eixo Y) no mesmo ponto: a origem da coordenada.
![]()
- Pode ser classificada como uma função polinomial de primeiro grau.
- A função identidade atua como um elemento neutro da composição da função . Para que qualquer função composta com a função identidade resulte na própria função.
![]()
- O valor que
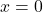
é a única raiz deste tipo de função.
- O limite da função identidade quando x tende para mais infinito ou menos infinito dá respectivamente mais infinito e menos infinito:
![]()
![]()
- A função identidade, portanto, não tem assíntota.
- A derivada da função identidade é a função constante com valor 1:
![]()
- A integral da função identidade é a função quadrática:
![]()
➤ Veja: fórmula da função quadrática