Aqui você aprenderá o que é a regra da cadeia e como derivar funções usando a regra da cadeia. Além disso, você poderá ver vários exemplos de derivadas resolvidas com a regra da cadeia e ainda poderá praticar com exercícios resolvidos passo a passo sobre derivadas aplicando a regra da cadeia.
Qual é a regra da cadeia?
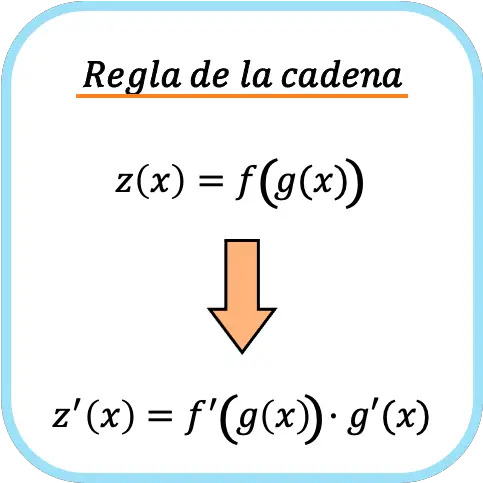
A regra da cadeia é uma fórmula usada para derivar funções compostas. A regra da cadeia afirma que a derivada de uma função composta f(g(x)) é igual à derivada f'(g(x)) multiplicada pela derivada g'(x) .
➤ Veja: função composta
Informalmente, costuma-se dizer que a regra da cadeia consiste em diferenciar a função e depois multiplicá-la pelo que está nela .
A fórmula da regra da cadeia permite-nos diferenciar funções compostas com muito mais facilidade, porque se diferenciássemos uma composição de funções utilizando o limite da definição da derivada, teríamos que fazer muitos cálculos.
Por outro lado, deve-se levar em consideração que esta regra só é utilizada para encontrar a derivada de funções compostas, e não de qualquer tipo de função ou operações com funções. Por exemplo, um erro muito comum é errar e aplicar a regra da cadeia em produtos funcionais como os seguintes:
![]()
❌
A regra da cadeia só pode ser usada quando temos uma função dentro de outra .
![]()
✅
Exemplos de derivadas com a regra da cadeia
Dada a definição da regra da cadeia, derivaremos várias funções com a regra da cadeia como exemplo. Lembre-se que se em algum exemplo você não entender como a função é derivada com a regra da cadeia, pode nos perguntar nos comentários!
Exemplo 1
Neste exemplo, usaremos a regra da cadeia para derivar o logaritmo natural de x ao quadrado:
![]()
A derivada do logaritmo natural é igual a 1 vezes o seu argumento, então a derivada
![]()
ser:
![]()
![]()
Por outro lado, a derivada de x elevada à potência de dois é 2x:
![]()
Finalmente, calculamos a derivada de toda a função aplicando a regra da cadeia. A derivada da função composta será o produto das duas derivadas que acabamos de encontrar:
![]()
![]()
Exemplo 2
Neste segundo exemplo, derivaremos uma função potencial baseada em um polinômio:
![]()
Para derivar uma potência, precisamos colocar o expoente original na frente dele e subtrair uma unidade do expoente, de modo que a derivada da função potencial sem aplicar a regra da cadeia seria:
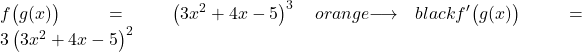
Agora deduzimos o que está entre parênteses:
![]()
E por fim, utilizamos a regra da cadeia para resolver a derivada de toda a função, que será a multiplicação das duas derivadas calculadas anteriormente:
![]()
![]()
Exemplo 3
Neste caso, resolveremos a derivada seno de x ao cubo mais 7x:
![]()
Na verdade, é uma composição de funções porque temos a função x 3 +7x dentro da função seno, podemos portanto usar a regra da cadeia para encontrar a derivada da função composta.
Por um lado, a derivada do seno é o cosseno, então a derivada da função exterior será o cosseno com o mesmo argumento do seno:
![]()
E por outro lado, a derivada de x 3 +7x é 3x 2 +7.
![]()
Portanto, a derivada da função composta é o produto das duas derivadas:
![]()
![]()
Exercícios resolvidos sobre derivadas com a regra da cadeia
Exercício 1
Derive a seguinte função composta usando a regra da cadeia:
![]()
A função exterior é uma função potencial, portanto para calcular sua derivada deve-se aplicar a seguinte fórmula:
![]()
![]()
E então calculamos a derivada da função interna. É uma subtração de potências, portanto para calcular sua derivada deve-se aplicar a seguinte fórmula a cada um de seus termos:
![]()
![]()
![]()
Resumindo, a derivada da função composta é o produto das duas derivadas encontradas:
![]()
![]()
Exercício 2
Resolva a derivada da seguinte função composta usando a regra da cadeia:
![]()
Primeiro, encontramos a derivada da função exterior:
![Rendered by QuickLaTeX.com \begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e5d21c7196c7ebaeaf6ca11762ca251_l3.png)
E agora resolvemos a derivada da função interior:
![]()
A derivada de toda a função é, portanto:
![]()
![]()
Exercício 3
Calcule a derivada da seguinte composição de funções com a regra da cadeia:
![]()
É uma função exponencial, portanto para calcular sua derivada deve-se aplicar a seguinte fórmula:
![]()
![]()
Também diferenciamos a função do expoente da função:
![]()
E usamos a regra da cadeia para encontrar a derivada da função composta inteira:
![]()
![]()
Exercício 4
Encontre a derivada da seguinte função composta usando a regra da cadeia:
![]()
Esta é uma composição de funções, pois temos uma função senoidal e uma função linear no argumento de uma função irracional. Então primeiro calculamos a derivada da raiz:
![]()
![Rendered by QuickLaTeX.com f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e909efbe50930f94cce0b2485b060046_l3.png)
E agora derivamos o argumento do radical. É uma soma de funções, então a derivada será a soma das derivadas de cada termo:
![]()
Assim, a derivada de toda a função é igual à multiplicação das duas derivadas calculadas:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fad132b49a5faab86a3955efd5422973_l3.png)
Exercício 5
Derive a seguinte composição de funções usando a regra da cadeia:
![]()
Para aplicar a regra da cadeia, você deve encontrar a derivada da potência e do polinômio e depois multiplicá-los. Assim, derivamos a potência usando a fórmula correspondente:
![]()
![]()
Segundo, derivamos a função polinomial do expoente:
![]()
E a regra da cadeia nos diz que a derivada de toda a função é o produto das derivadas que acabamos de encontrar:
![]()
![]()
Exercício 6
![]()
Obviamente, a função neste problema é composta, pois no argumento do logaritmo natural temos o produto de dois tipos diferentes de funções. Então primeiro diferenciamos o logaritmo:
![]()
![]()
Segundo, derivamos a função do argumento do logaritmo. Esta é uma multiplicação de duas funções, então você deve usar a seguinte fórmula para fazer a derivação:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-643ddf7ec82cbcc3bc685ceadf59da98_l3.png)
Assim, a derivada de toda a função, segundo a regra da cadeia, será o produto das duas derivadas:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6912d0951fb85a61df21cbed282000f2_l3.png)
Exercício 7
Resolva a derivada da seguinte função usando a regra da cadeia:
![]()
Esta é uma composição de funções, portanto vamos diferenciar o logaritmo e seu argumento separadamente e depois multiplicar as derivadas.
Então, primeiro, diferenciamos o logaritmo na base 9:
![]()
![]()
E agora calculamos a derivada do argumento do logaritmo. Observe que o número e possui uma função em seu argumento, ou seja, é uma função composta, portanto também precisamos aplicar a regra da cadeia para derivar esta função:
![]()
![]()
Assim, a derivada do argumento inteiro do logaritmo será:
![]()
E finalmente, a derivada de toda a função será o produto de f'(g(x)) e g'(x):
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a702df902c9f1eff66e14836a262c0a_l3.png)
Exercício 8
Derive a seguinte função composta usando a regra da cadeia:
![]()
Neste exercício temos uma composição de diversas funções, portanto teremos que aplicar a regra da cadeia diversas vezes. Primeiro derivamos a função trigonométrica do seno, cuja derivada é cosseno:
![]()
E agora calculamos a derivada do argumento do seno usando a regra da cadeia:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e1c2492990456e277e493c898cb3924_l3.png)
Finalmente, obtemos a derivada de toda a composição de funções aplicando novamente a regra da cadeia:
![]()
![]()
Prova de Regra da Cadeia
Finalmente, provaremos a fórmula da regra da cadeia. Para fazer isso, partiremos da definição matemática de uma derivada:
![]()
Seja z uma função composta por duas funções:
![]()
Então a derivada da função z aplicando a definição seria:
![]()
Como você já sabe, você pode multiplicar e dividir uma fração pelo mesmo termo, pois isso não altera o resultado. Podemos, portanto, passar para a próxima etapa:
![]()
Reorganizamos os denominadores das frações:
![]()
Ao aplicar as propriedades dos limites, podemos dividir o limite acima em dois. Como o limite de um produto é igual ao produto dos limites:
![]()
E esta expressão é equivalente ao seguinte:
![]()
A fórmula da regra da cadeia está, portanto, comprovada, uma vez que chegamos a ela a partir da definição da derivada.