Neste artigo explicamos o que são funções simétricas (funções pares e ímpares) e como estudar a simetria de uma função. Você também poderá ver as propriedades desses tipos de funções e, por fim, poderá praticar com exercícios resolvidos passo a passo de funções simétricas.
O que é uma função simétrica?
Uma função simétrica é uma função na qual um eixo de simetria pode ser encontrado em sua representação gráfica. Existem dois tipos de funções simétricas: funções pares, simétricas em relação ao eixo Y, e funções ímpares, simétricas em relação à origem das coordenadas.
Lembre-se de que um eixo de simetria é uma linha imaginária que divide qualquer coisa em duas partes de modo que seus pontos opostos sejam equidistantes um do outro.
funções pares
Funções pares são funções simétricas em relação ao eixo y, ou seja, o eixo Y é um eixo de simetria da função.
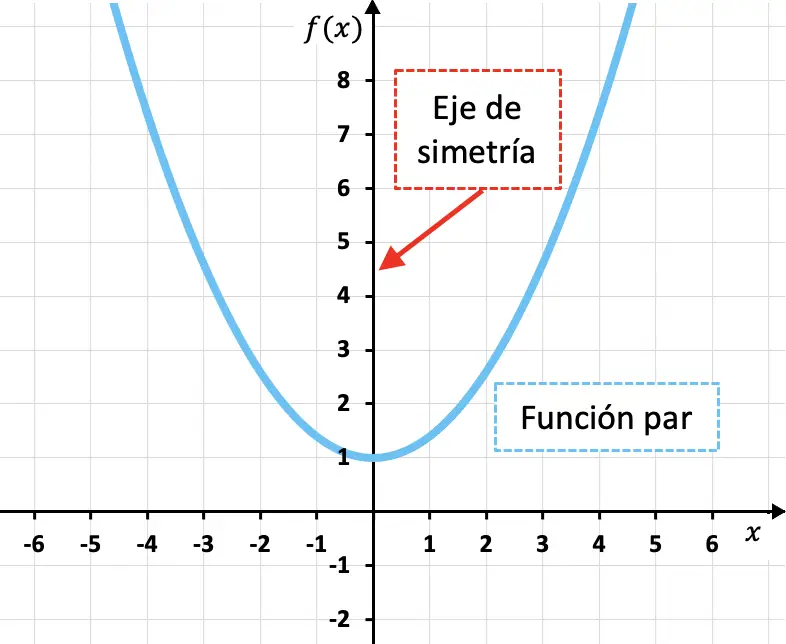
Como você pode ver na função quadrática mostrada acima, a imagem de uma função par para qualquer valor da variável independente (x) é equivalente à imagem da função para o valor oposto (-x). Em outras palavras, matematicamente, uma função é par se atender à seguinte condição:
![]()
Funções pares são um tipo de função simétrica, agora vamos ver como são as funções ímpares.
funções estranhas
Funções ímpares são funções simétricas em relação à origem das coordenadas, ou seja, em relação ao ponto (0,0).
Abaixo você pode ver uma função estranha representada graficamente:
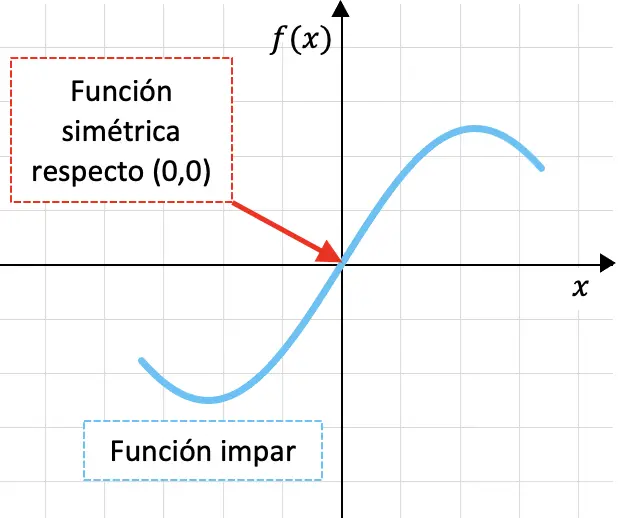
O fato de uma função ser simétrica em relação à origem das coordenadas significa que se dobrarmos o gráfico da função primeiro pelo eixo OY e depois pelo eixo OX, o gráfico da função se sobreporia.
Algebricamente, uma função é ímpar se a seguinte relação entre suas imagens for satisfeita:
![]()
Conhecer a simetria de uma função é muito útil para representá-la, pois conhecendo apenas metade do gráfico podemos desenhar rapidamente a outra parte.
Como encontrar a simetria de uma função
Para estudar a simetria de uma função, devemos calcular a imagem de
![]()
, ou seja, é necessário calcular
![]()
Então, dependendo do resultado da imagem, a simetria da função será:
- se estiver preenchido
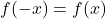
, a função é par e, portanto , simétrica em relação ao eixo Y.
- se estiver preenchido
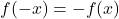
, a função é ímpar e, portanto , simétrica em relação à origem das coordenadas.
- Se nenhuma das condições acima for atendida, é uma função assimétrica (não possui eixo de simetria).
Por exemplo, vamos analisar a simetria da seguinte função cúbica:
![]()
Para estudar a simetria da função, calculamos
![]()
![]()
A expressão algébrica resultante é equivalente à expressão da função original, mas mudou de sinal, ou em outras palavras, a seguinte igualdade é satisfeita:
![]()
A função é, portanto, ímpar e, portanto, simétrica em relação à origem das coordenadas (0,0).
Propriedades de funções simétricas
As funções simétricas possuem as seguintes características:
- A soma de duas funções pares/ímpares é igual a outra função par/ímpar.
- O produto de duas funções pares ou de duas funções ímpares dá uma função par.
- A derivada de uma função par/ímpar é uma função par/ímpar.
- A composição entre duas funções pares/ímpares é equivalente a uma função par/ímpar.
- A única função par e ímpar, ou seja, simétrica em relação ao eixo OY e em relação à origem, é a função
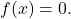
Problemas resolvidos de simetria de uma função
Exercício 1
Encontre a simetria da seguinte função:
![]()
Para calcular a simetria da função, precisamos avaliar
![]()
![]()
Qualquer potência de um número negativo elevado a um expoente dá um número positivo, então neste caso a seguinte equação é verdadeira:
![]()
A função é, portanto, par e, portanto, simétrica em relação ao eixo y (eixo Y).
Exercício 2
Estude a simetria da seguinte função racional:
![]()
Para determinar a simetria da função, fazemos
![]()
![]()
Neste problema, nenhuma condição de simetria é atendida, porque a imagem de
![]()
não é igual a
![]()
nem para
![]()
![]()
A função, portanto, não possui um eixo de simetria, mas é antes uma função assimétrica.
Exercício 3
Calcule a simetria da seguinte função:
![]()
Para analisar a simetria da função, precisamos calcular
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
Neste caso, a expressão resultante é semelhante à expressão original, mas com mudança de sinal, de modo que a seguinte equação é cumprida:
![]()
A função é, portanto, ímpar e, portanto, simétrica em relação à origem das coordenadas (0,0).