Neste artigo explicamos o que é uma função constante e qual a sua representação gráfica. Além disso, você poderá ver diversos exemplos de funções constantes e todas as características deste tipo de função. E, por fim, você poderá treinar com exercícios resolvidos de funções constantes.
O que é uma função constante?
Uma função constante é aquela função que sempre assume a mesma imagem para qualquer valor da variável independente (x) , ou seja, uma função constante tem a forma f(x)=k , onde k é um número real qualquer.
![]()
A representação gráfica de uma função constante é uma linha horizontal.
Por exemplo, todas as funções a seguir são constantes:
![]()
Representação gráfica de uma função constante
Depois de vermos o conceito de função constante, veremos como representar uma função constante em um gráfico.
Representar graficamente uma função constante é bastante simples, basta desenhar uma linha horizontal no valor da função (k).
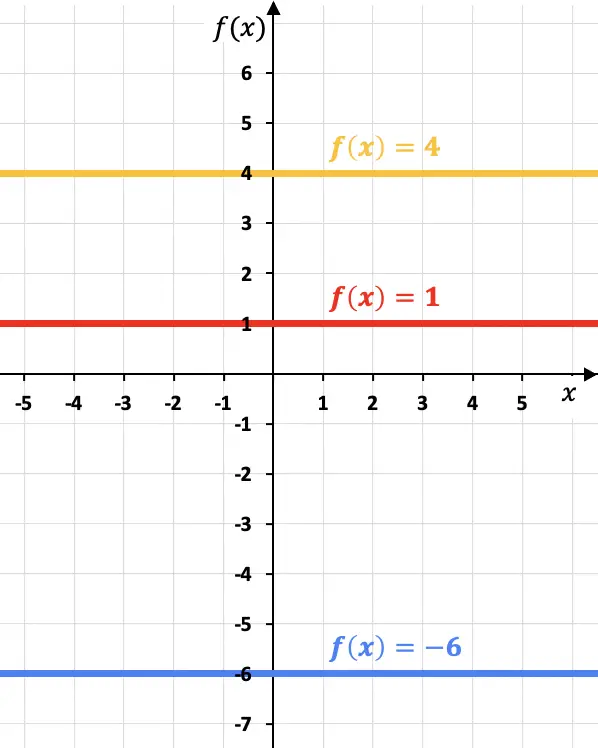
Veja os exemplos a seguir nos quais representamos três funções constantes diferentes em um gráfico:

Observe que cada função constante é paralela ao eixo x.
Por outro lado, deve-se ter em mente que uma linha vertical não é uma função constante. Na verdade, uma linha vertical nem sequer é uma função, pois por definição uma função só pode ter uma imagem para cada valor de x.
Características da função constante
A seguir, analisaremos as propriedades da função constante. Considere uma função constante de qualquer valor:
![]()
- O domínio da função constante são todos os números reais:
![]()
- O caminho ou intervalo da função constante é apenas o valor da constante:
![]()
- É uma função contínua e par, porque a função sempre assume o mesmo valor:
![]()
- A função constante não é crescente nem decrescente, é um tipo de função que sempre tem inclinação zero:
![]()
- Sempre cruza o eixo OY no ponto (0,k).
![]()
- Toda função constante é um polinômio de grau zero.
- Sim
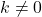
a função constante não tem raiz, em vez disso, se
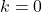
todos os números reais são raízes da função constante.
- O limite da função constante quando x se aproxima de mais infinito ou menos infinito é igual ao valor da constante:
![]()
![]()
- A derivada da função constante é sempre zero:
![]()
Na verdade, a definição da função constante também pode ser feita a partir da noção de derivada: uma função é constante se a sua derivada desaparece em todo o seu domínio.
- A integral da função constante é a função linear (ou afim):
![]()
➤ Veja: O que é uma função linear?
Função constante em um intervalo
Vimos como uma função é constante, porém, uma função só pode ser constante num intervalo do seu domínio.
Para entender este conceito, você precisa saber quais funções são definidas em chunks, então antes de continuar recomendamos dar uma olhada na seguinte explicação:
➤ Veja: O que é uma função por partes?
Depois de saber o que são esses tipos de funções, observe a função definida nas partes mostradas abaixo:

Como você pode ver no gráfico, a função não é constante em todos os números em seu domínio. Mas é constante no intervalo [-2,4), portanto é uma função constante apenas em um intervalo.
Problemas corrigidos de função constante
Exercício 1
Identifique quais das seguintes funções são constantes:
![]()
A primeira função,
![]()
, é uma função constante, pois é sempre 4, qualquer que seja o valor que a variável x assume.
A segunda função,
![]()
, não é uma função constante porque o valor da função varia dependendo do valor de x. É uma função afim.
A terceira função,
![]()
, é sempre igual a 0 para qualquer valor de x, portanto é de fato uma função constante.
A quarta função,
![]()
, não é uma função constante porque varia dependendo do valor de x. É uma função linear.
Exercício 2
Encontre a função constante que passa pelo ponto (0,6).
Algebricamente, a fórmula da função constante tem sempre a mesma forma:
![]()
E graficamente a função constante é sempre uma reta horizontal, portanto, as coordenadas de uma função constante são sempre iguais e de valor
![]()
Como o ponto pelo qual a função passa tem coordenada y=6, a função constante que procuramos neste problema deve ser:
![]()
Exercício 3
Trace as seguintes funções constantes no mesmo gráfico:
![]()
Para representar cada função constante, basta desenhar uma linha reta horizontal na altura de cada constante: