Neste artigo explicamos o que são funções limitadas (superiores e inferiores). Além disso, mostraremos o que significa uma função ser limitada em um ponto e, por fim, você encontrará as propriedades desse tipo de função.
O que é uma função limitada?
Uma função limitada é uma função cujo gráfico está dentro dos limites. Ou seja, uma função é limitada acima se existe um número K tal que não há valor da função maior que K (f(x)≤K), e uma função é limitada abaixo se existe um número K tal que é menor que todos os valores da função (f(x)≥K). Portanto, uma função limitada é uma função limitada acima e abaixo.
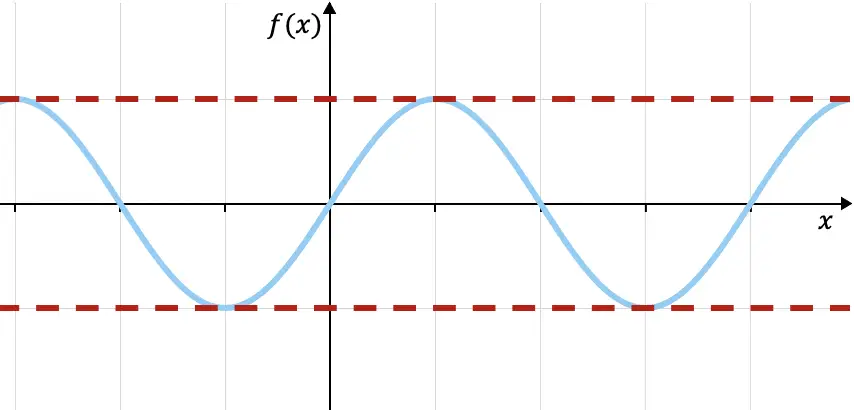
Por exemplo, a função seno trigonométrica, representada graficamente acima, é limitada na parte superior por f(x)=1 e é limitada na parte inferior por f(x)=-1 (linhas pontilhadas vermelhas), uma vez que todos os valores do função estão dentro desses dois limites. Você pode ver mais propriedades desta função no seguinte link:
➤ Veja: Características da função seno
função limitada acima
No entanto, nem todas as funções são limitadas acima e abaixo; uma função só pode ser limitada acima ou abaixo.
As funções limitadas acima são aquelas que não ultrapassam um determinado valor, ou seja, a seguinte condição é atendida:
![]()
onde o valor K é o limite superior da função.
Por exemplo, a seguinte parábola é limitada na parte superior por K=7, mas a função não é limitada na parte inferior, uma vez que os seus ramos se estendem até ao infinito.

Logicamente, se a função for limitada por K=7, ela também será limitada por K=8 e valores superiores.
O menor limite superior é chamado de limite superior e é representado por sup(f) . Além disso, se a função atingir o referido limite superior no seu domínio, diremos que este ponto é o máximo absoluto da função.
➤ Veja: quais são os máximos e mínimos de uma função?
No nosso caso, a função é geometricamente limitada por K=7, sendo portanto o extremo superior e o máximo absoluto da função.
função delimitada abaixo
As funções delimitadas a seguir são aquelas que não possuem valor inferior a um determinado número, ou seja, satisfazem a seguinte expressão matemática:
![]()
Onde o valor K é o limite inferior da função.
Abaixo você tem a representação gráfica de uma função exponencial que é delimitada abaixo por K=3:

Obviamente, a função também é limitada por valores menores que K=3.
Como antes, o maior limite inferior é chamado de limite inferior e é representado por inf(f) . Além disso, se a função atingir o referido extremo inferior no seu domínio, diremos que este ponto é o mínimo absoluto da função.
Neste caso, K=3 não é o mínimo absoluto da função, pois a função atinge este valor no infinito e, portanto, está fora do seu domínio. Em outras palavras, f(x)=3 é uma assíntota horizontal da função .
Existe um teorema que permite saber se uma função é limitada na parte superior e inferior sem sua representação gráfica. Clique aqui para ver o que é o teorema de Weierstrass.
➤ Veja: Teorema de Weierstrass
Função limitada em um ponto
Acabamos de estudar a noção de delimitação de uma função em geral, mas também é possível analisar se uma função é ou não limitada numa vizinhança menor, ou seja, numa parte da função.
Sim
![]()
é um ponto no domínio da função e
![]()
qualquer valor, diremos que a função é limitada acima/abaixo no ponto
![]()
se houver um ambiente
![]()
onde a função é limitada acima/abaixo.
Portanto, uma função é limitada no ponto
![]()
se for delimitado na parte superior e inferior de uma vizinhança
![]()
Obviamente, se uma função é limitada em geral, também o será em cada um dos seus pontos. Porém, o oposto é falso, ou seja, uma função pode ser limitada em cada um dos seus pontos e não em todo o seu domínio.
Por exemplo, a seguinte função afim é parcialmente limitada em cada um dos seus pontos, mas não é uma função limitada.

Propriedades de funções limitadas
Funções limitadas têm as seguintes propriedades:
- Sim

E

são duas funções limitadas, a adição (ou subtração) das duas funções
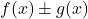
também é uma função limitada.
- Sim

E

são duas funções limitadas, o produto das duas funções
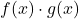
também é uma função limitada.
- Se uma função tiver uma assíntota vertical, ela não pode ser totalmente limitada. Por outro lado, a função pode ser limitada acima ou abaixo.
- Qualquer função contínua e limitada em um intervalo é integrável.