Nesta página você encontrará tudo sobre a função tangente: o que é, qual a sua fórmula, como representá-la em um gráfico, as características da função, seu período, etc. Além disso, você poderá ver exemplos de funções tangentes para compreender totalmente o conceito. Ele ainda explica o teorema da tangente e as relações que a função tangente tem com outras relações trigonométricas.
Fórmula da função tangente
A função tangente de um ângulo α é uma função trigonométrica cuja fórmula é definida como a razão entre o ramo oposto e o ramo contíguo (ou adjacente) de um triângulo retângulo (triângulo com ângulo reto).

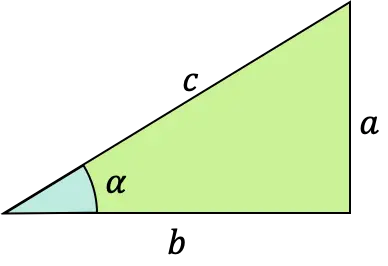
Este tipo de função matemática também é chamada de função tangentóide, tangenóide ou tangencial. E pode ser expresso com a abreviatura “tg” ou mesmo “tan”.
A função tangente é uma das três razões trigonométricas mais conhecidas, junto com o seno e o cosseno de um ângulo.
Valores característicos da função tangente
Existem certos ângulos que se repetem frequentemente e, portanto, é conveniente saber o valor da função tangente nestes ângulos:
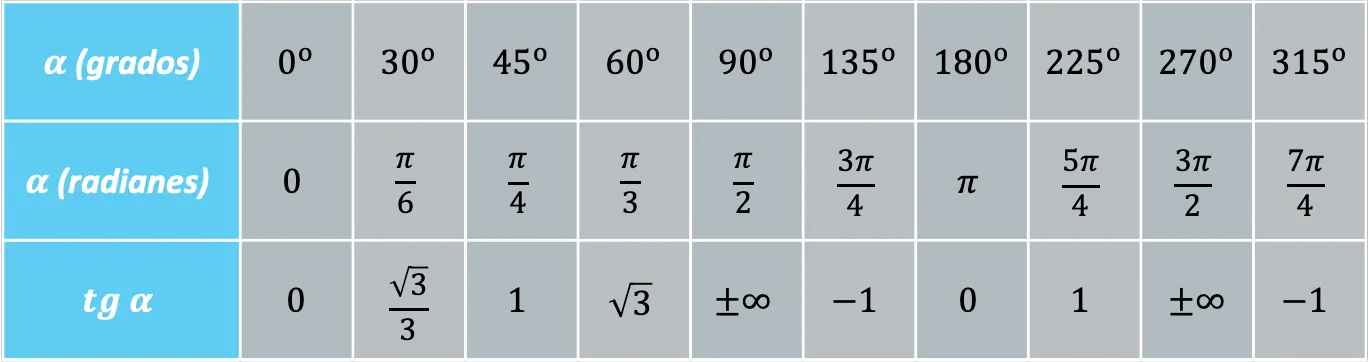
Por outro lado, a função tangente pode ser ligada às funções seno e cosseno pela seguinte identidade trigonométrica fundamental:
![]()
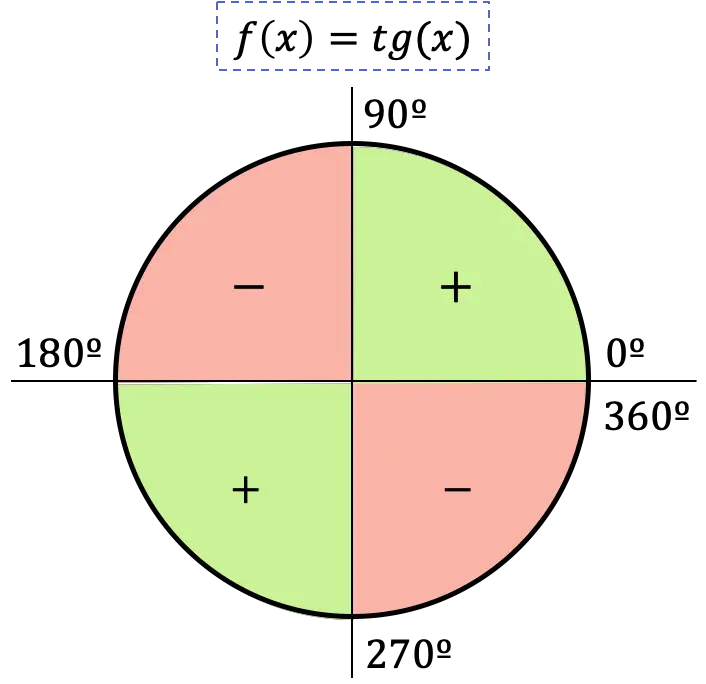
Assim, o sinal da função tangente depende do quadrante em que o ângulo está localizado:
- Se o ângulo pertencer ao primeiro quadrante, sua tangente será positiva, pois neste quadrante o seno e o cosseno também são positivos.
- Se o ângulo cair no segundo quadrante, sua tangente será negativa, pois neste quadrante o seno é positivo mas o cosseno é negativo.
- Se o ângulo estiver no terceiro quadrante, sua tangente será positiva, pois neste quadrante o seno e o cosseno são negativos.
- Se o ângulo estiver no quarto quadrante, sua tangente será negativa, pois neste quadrante o seno é negativo e ao invés o cosseno é positivo.
Representação gráfica da função tangente
Com a tabela de valores que vimos na seção anterior, podemos representar graficamente a função tangente. E fazendo o gráfico da função tangente, obtemos:
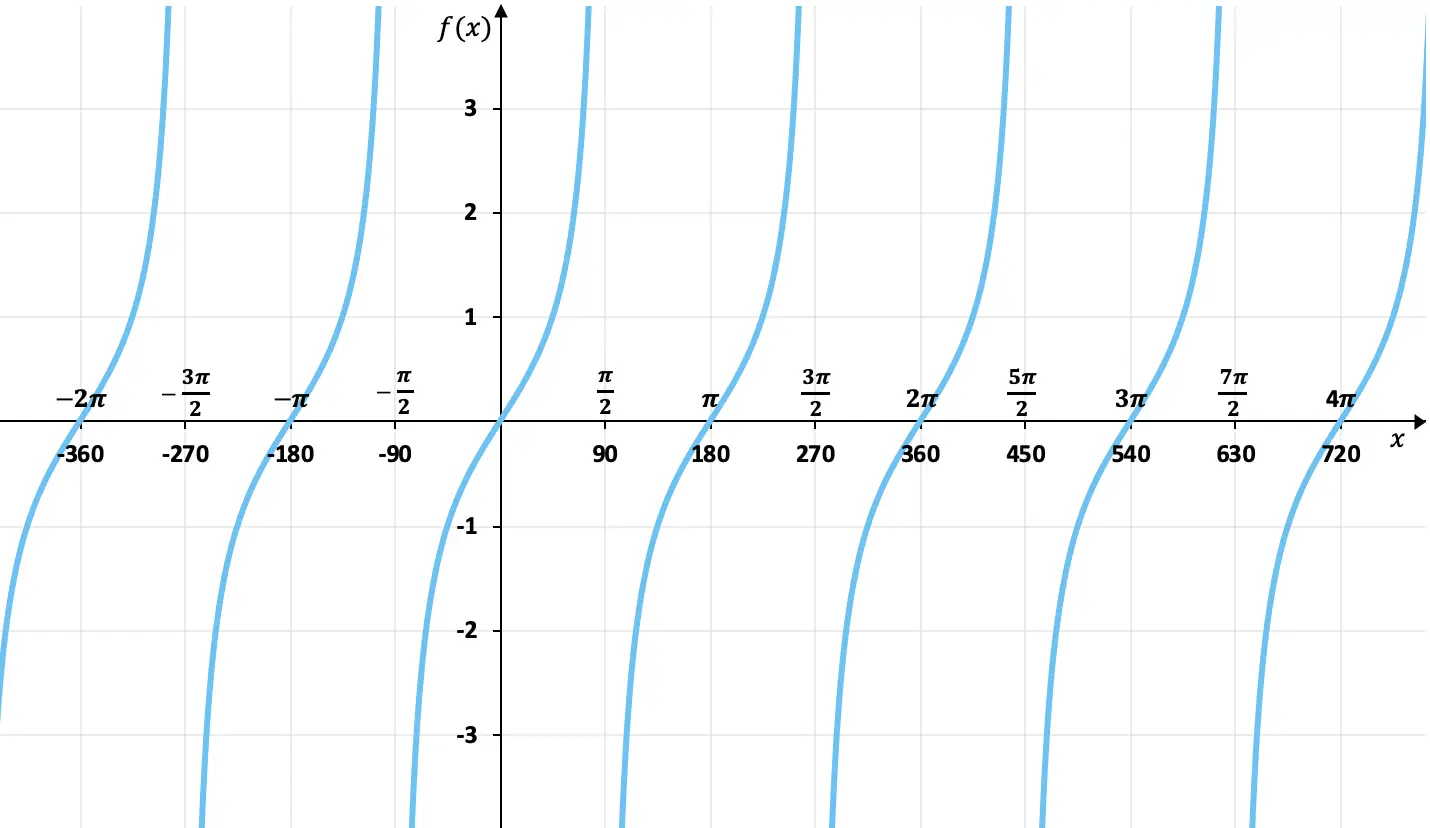
Como pode ser visto no gráfico, os valores das imagens da função tangente não são limitados, ao contrário das funções seno e cosseno. Além disso, os valores se repetem a cada 180 graus (π radianos), portanto é uma função periódica cujo período é 180º.
Por outro lado, neste gráfico podemos ver que a função tangente é ímpar , pois seus elementos opostos possuem imagens opostas, ou seja, é simétrica em relação à origem (0,0). Por exemplo, a tangente de 45° vale 1 e a de -45° vale -1.
Finalmente, também podemos ver que a função tangente possui assíntotas verticais . Por exemplo, chega muito perto da linha x=90º, mas nunca a toca, e a mesma coisa acontece a cada 180 graus. Isso significa que o limite da função nesses pontos tende ao infinito.
Propriedades da função tangente
A função tangente possui as seguintes características:
- O domínio da função tangente são todos os números reais, exceto os pontos onde há uma assíntota vertical:
![]()
![]()
- O contradomínio ou contradomínio da função tangente são todos números reais.
![]()
- É uma função contínua e ímpar com periodicidade π.
![]()
- Este tipo de função trigonométrica possui um único ponto de intersecção com o eixo y (eixo Y) no ponto (0,0).
![]()
- Em vez disso, ele intercepta periodicamente a abcissa (eixo X) em várias coordenadas de pi.
![]()
- A função é estritamente crescente em todo o domínio, portanto não tem máximo nem mínimo.
- A derivada da tangente é:
![]()
- Finalmente, a integral da função tangente é:
![]()
Período da função tangente
Ao contrário de outras funções trigonométricas, como seno e cosseno, a função tangente não tem magnitude, pois não tem valor máximo nem mínimo. Porém, é uma função periódica, ou seja, seus valores se repetem com uma frequência como vimos em seu gráfico.
![]()
- O período da função tangente é a distância entre dois pontos nos quais o gráfico se repete e é calculado com a seguinte fórmula:
![]()
teorema da tangente
Embora a fórmula da tangente seja normalmente usada em triângulos retângulos, existe também um teorema que pode ser aplicado a qualquer tipo de triângulo: o teorema da tangente.
O teorema da tangente relaciona os lados e ângulos de qualquer triângulo da seguinte forma:
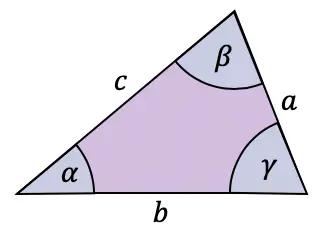
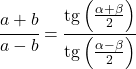
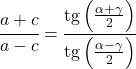
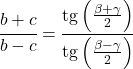
Relações da função tangente com outras razões trigonométricas
Abaixo você encontra as relações da tangente com as razões trigonométricas mais importantes da trigonometria.
Relação com o seio
- A tangente e o seno de um ângulo estão relacionados da seguinte forma:
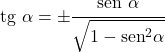
Razão cosseno
- Da mesma forma, a tangente e o cosseno de um ângulo estão relacionados à seguinte igualdade:
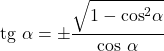
Relação com a cossecante
- Embora seja difícil de provar, a tangente pode ser resolvida de modo que dependa apenas da cossecante:
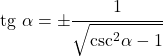
Relação com a secante
- A tangente e a secante de um ângulo estão relacionadas pela seguinte equação:
![]()
Relação com a cotangente
- Tangente e cotangente são inversos multiplicativos:
![]()