Esta página explica o que são funções de proporcionalidade inversa e como representá-las graficamente. Além disso, você encontrará todas as características desse tipo de função, como calcular seu domínio e também diversos exemplos e exercícios resolvidos passo a passo para praticar.
O que é uma função de proporcionalidade inversa?
Uma função de proporcionalidade inversa é uma função que relaciona duas grandezas inversamente proporcionais, ou seja, uma grandeza aumenta quando a outra diminui e vice-versa. Em geral, as funções de proporcionalidade inversa são definidas pela seguinte fórmula:
![]()
Ouro
![]()
é uma constante chamada razão de proporcionalidade.
Assim, as funções de proporcionalidade inversa são sempre compostas por frações com polinômio de primeiro grau no denominador. Portanto, eles são um tipo de função racional.
Exemplos de funções de proporcionalidade inversa:
![]()
Geralmente
![]()
é geralmente a variável independente e
![]()
a variável dependente, ou em outras palavras, a variável
![]()
depende de
![]()
Por outro lado, a razão de proporcionalidade (termo do numerador) pode ser positiva ou negativa e seu sinal marca o aumento ou diminuição da função:
- Se a constante

é negativo, a função é crescente.
- Em vez disso, se a constante

é positivo, a função está diminuindo.
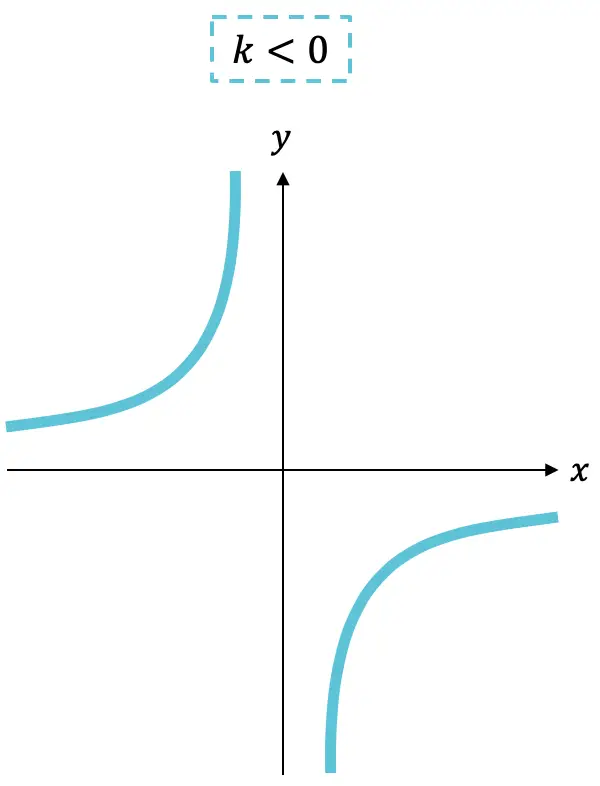
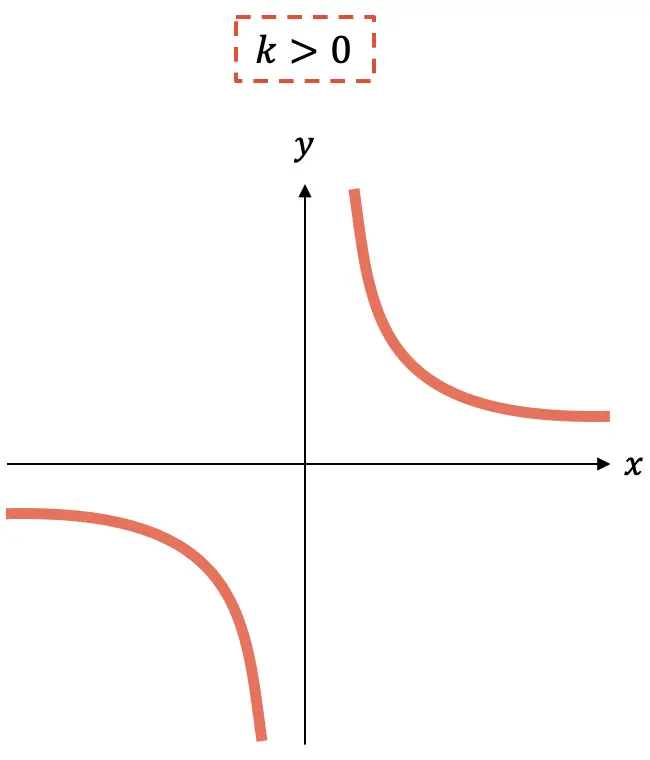
Como você pode ver, o gráfico de uma função de proporcionalidade inversa consiste sempre em duas hipérboles que, dependendo do sinal de k , estarão em um quadrante ou outro.
Domínio de uma função de proporcionalidade inversa
Sendo um tipo de função racional, o domínio de uma função de proporcionalidade inversa são todos os números reais exceto aqueles que desaparecem do denominador . Porque o denominador nunca pode ser zero porque isso resultaria no infinito.
Como exemplo, determinaremos o domínio da seguinte função de proporcionalidade inversa:
![]()
Para saber quando o denominador é zero, devemos igualar sua expressão a 0 e resolver a equação:
![]()
![]()
Assim, quando x assume o valor 1, o denominador será zero e obteremos indeterminação. Portanto, o domínio da função são todos os números reais menos
![]()
![]()
Como representar graficamente uma função de proporcionalidade inversa
Veremos como representar graficamente uma função de proporcionalidade inversa usando um exemplo.
- Representaremos a seguinte função em um gráfico:
![]()
A primeira coisa que precisamos fazer é encontrar o domínio da função. Sendo uma fração, o denominador nunca pode ser 0, porque isso resultaria no infinito. Portanto, o domínio será todo x, exceto quando o denominador for cancelado.
Portanto, definimos o denominador igual a 0 para ver qual x não pertence ao domínio:
![]()
![]()
Portanto, o domínio da função são todos os números, exceto 2:
![]()
Depois de sabermos qual número não pertence ao domínio, criamos uma tabela de valores. Para representar funções de proporcionalidade inversa é necessário calcular 3 ou 4 pontos à esquerda e 3 ou 4 pontos à direita do número que não pertence ao domínio (2):
![]()

Agora vamos representar os pontos em um gráfico :
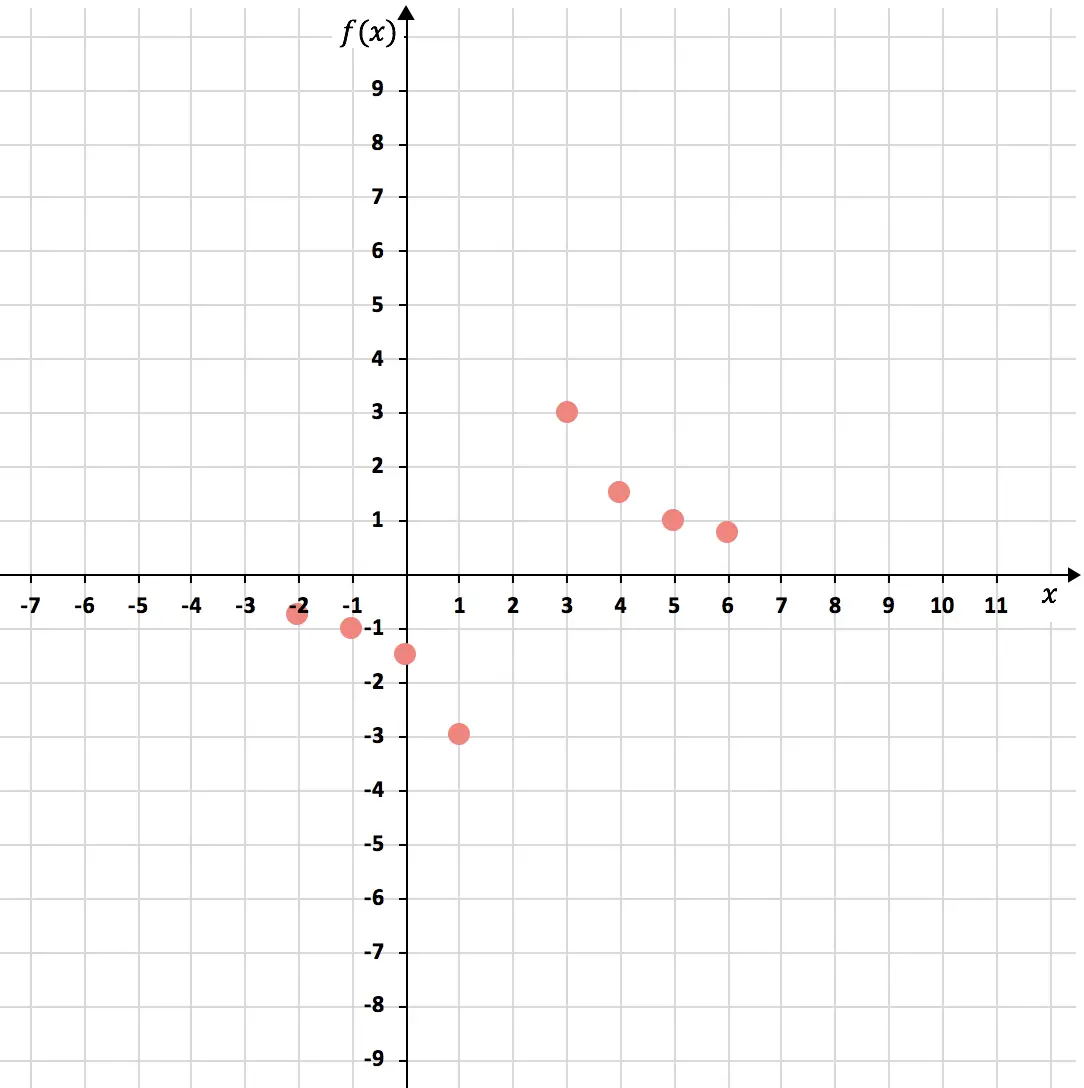
E por fim juntamos os pontos, formando as duas hipérboles da função de proporcionalidade inversa. Além disso, alongamos os ramos das hipérboles para indicar que elas continuam a crescer:

Observe que a função se aproxima
![]()
, tanto à direita quanto à esquerda. No entanto, nunca atinge 2, chega muito perto, mas nunca atinge. ENTÃO,
![]()
é uma assíntota vertical . É porque
![]()
não pertence ao domínio da função e, portanto, a função não existe nesse ponto.
E a mesma coisa acontece com o eixo horizontal X. A função se aproxima
![]()
mas nunca toque nele. Ainda,
![]()
é uma assíntota horizontal .
Isso significa que todas as funções de proporcionalidade inversa são descontínuas, porque sempre possuem uma assíntota.
Você pode aprender mais sobre assíntotas e limites de funções em nosso site.
Problemas resolvidos de funções de proporcionalidade inversa
Exercício 1
Calcule o domínio da seguinte função de proporcionalidade inversa:
![]()
Uma função de proporcionalidade inversa não existirá quando o denominador for 0, porque então a função produziria ∞. Portanto, precisamos igualar o denominador da função a 0 para ver que x cancela o denominador e, portanto, não pertence ao domínio.
![]()
![]()
![]()
![]()
Exercício 2
Faça um gráfico da seguinte função de proporcionalidade inversa:
![]()
A primeira coisa a fazer é calcular o domínio da função:
![]()
![]()
Depois de sabermos qual número não pertence ao domínio, criamos um array de valores com a função:

Por fim, representamos os pontos obtidos no gráfico e desenhamos as hipérboles, formando assim a função de proporcionalidade inversa:
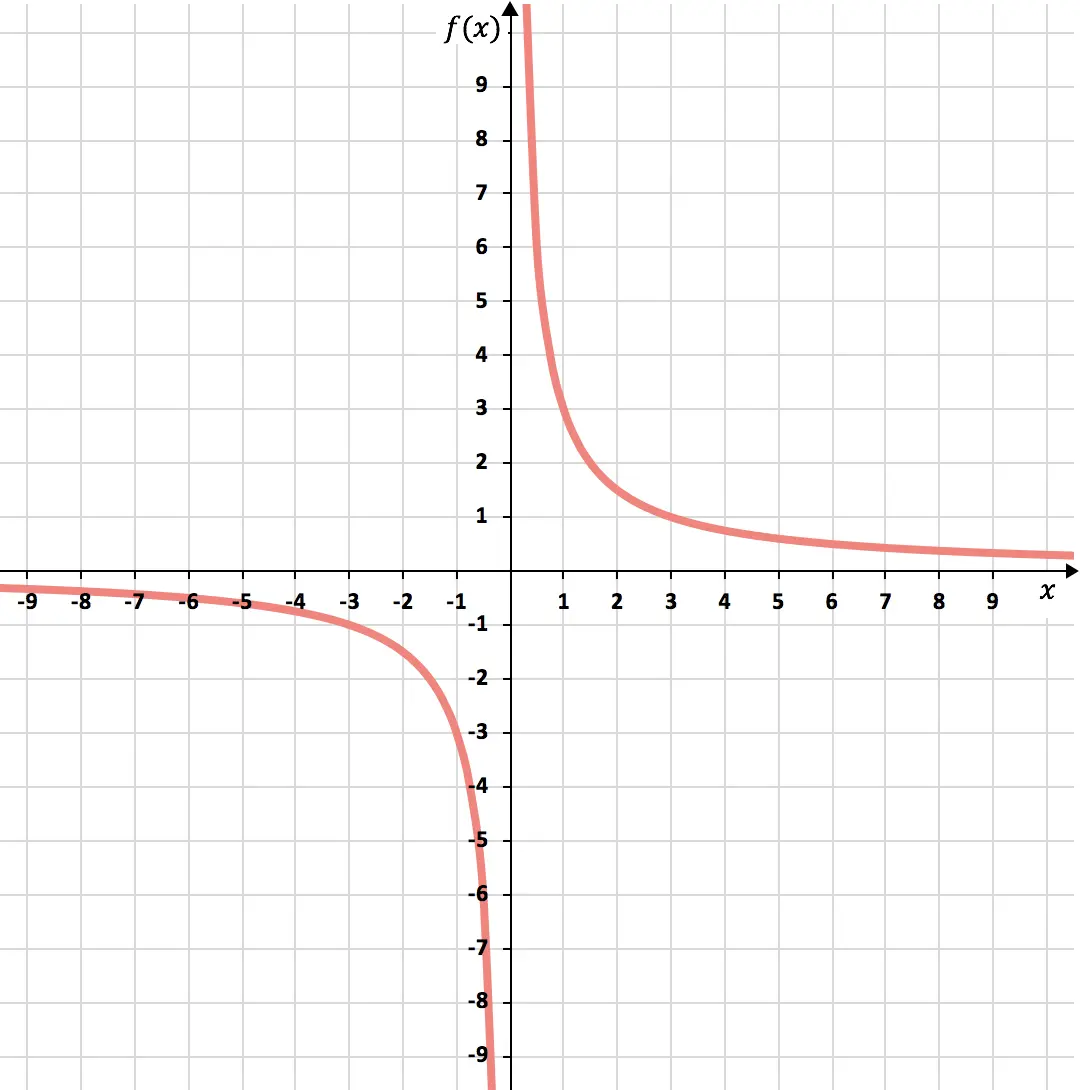
Exercício 3
Faça um gráfico da seguinte função de proporcionalidade inversa:
![]()
A primeira coisa a fazer é calcular o domínio da função:
![]()
![]()
![]()
Depois de conhecermos o domínio da função, construímos uma tabela de valores:

Por fim, representamos os pontos obtidos em um gráfico e plotamos as hipérboles, formando assim a função de proporcionalidade inversa:
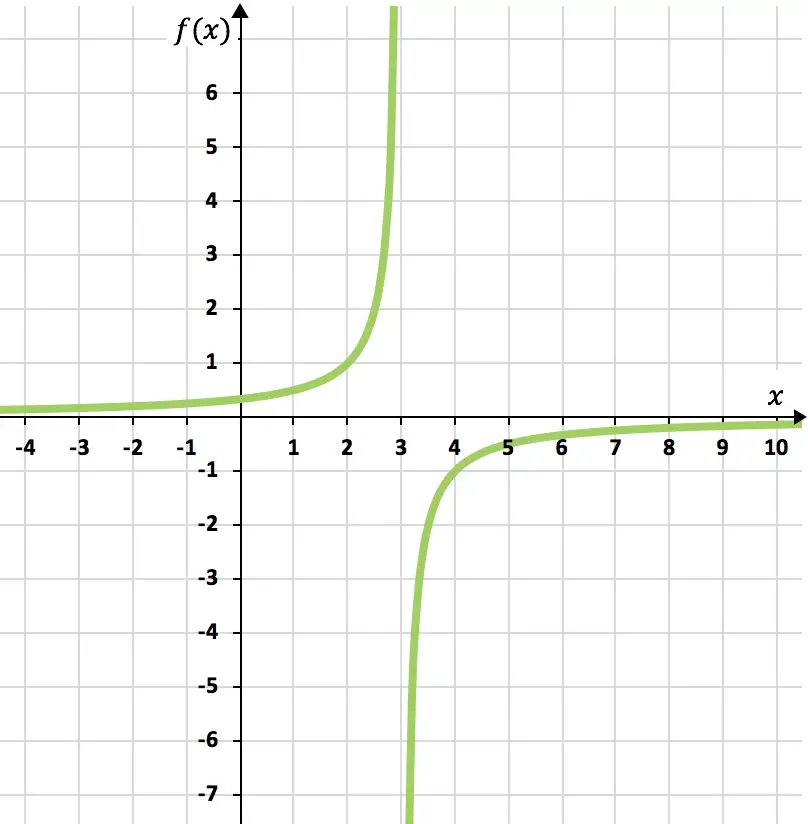
Exercício 4
Faça um gráfico da seguinte função de proporcionalidade inversa:
![]()
Primeiro precisamos calcular o domínio da função:
![]()
![]()
![]()
![]()
Depois de conhecermos o domínio da função, criamos uma matriz de valores:
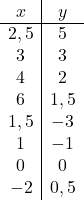
E, por fim, representamos os pontos obtidos em um gráfico e desenhamos as hipérboles, formando assim a função de proporcionalidade inversa:
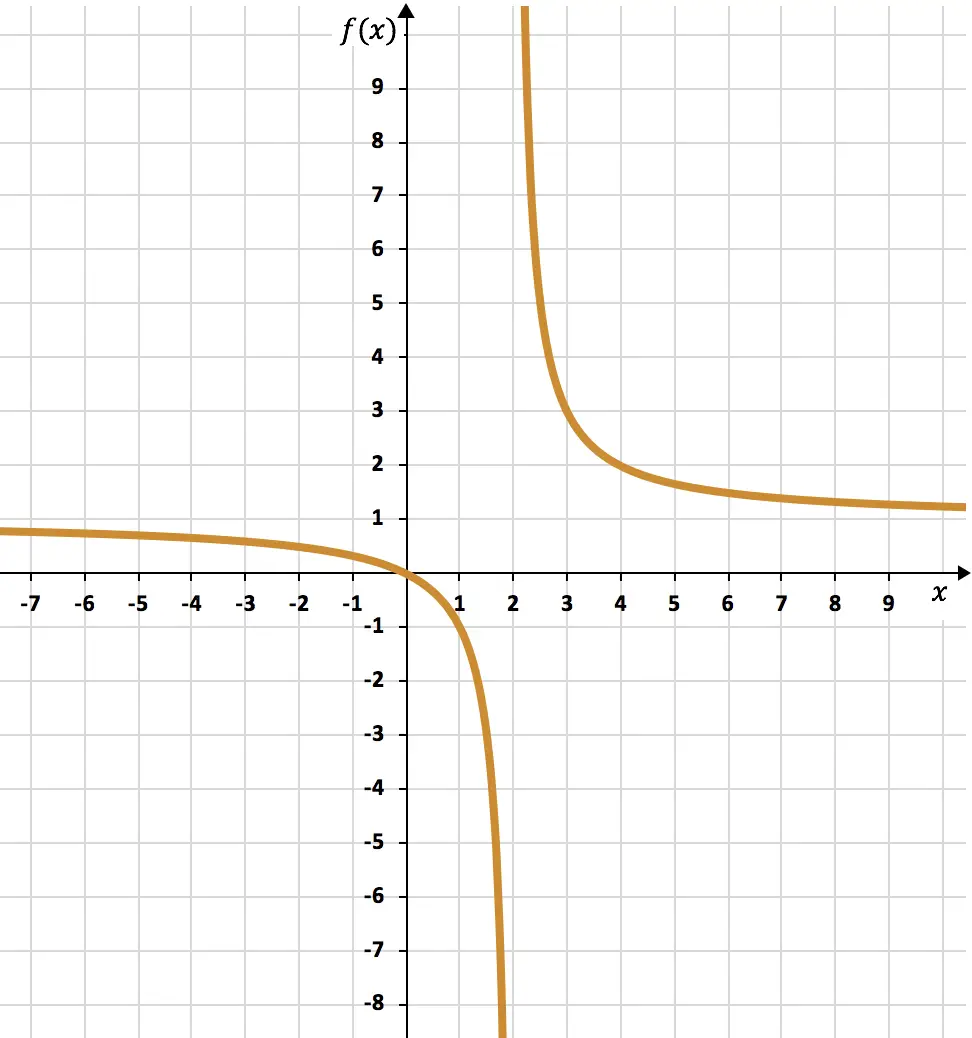
Exercício 5
Faça um gráfico da seguinte função racional:
![]()
A primeira coisa a fazer é calcular o domínio da função:
![]()
![]()
![]()
![]()
Depois de conhecermos o domínio da função, construímos uma tabela de valores:

Para finalizar, basta representar os pontos obtidos em um gráfico e desenhar as hipérboles, formando assim a função fracionária:

Aplicações da função de proporcionalidade inversa
A função de proporcionalidade inversa aparece em muitos casos na física e na matemática.
Por exemplo, é usado para descrever a relação entre pressão e volume em um gás ideal sujeito a uma temperatura constante k. Esta função é chamada de lei de Boyle-Mariotte (P×V=k) e é um exemplo de função de proporcionalidade inversa. Obviamente, o domínio de definição desta função limita-se apenas ao ramo positivo, uma vez que não existem volumes ou pressões negativas.
A relação entre intensidade de corrente e resistência elétrica sujeita a uma diferença de potencial constante também é governada por uma função de proporcionalidade inversa. Esta função é conhecida como lei de Ohm (V=I×R).