Nesta página explicamos o que são matrizes idempotentes. Também mostramos vários exemplos deste tipo de matrizes para que você entenda completamente. Além disso, você encontrará a fórmula para encontrar uma matriz idempotente e, por fim, todas as propriedades das matrizes idempotentes.
O que é uma matriz idempotente?
A definição de uma matriz idempotente é a seguinte:
Uma matriz idempotente é aquela matriz que, quando multiplicada por si mesma, dá como resultado a mesma matriz.
![]()
Portanto, qualquer potência de uma matriz idempotente é igual à própria matriz, independente do expoente:
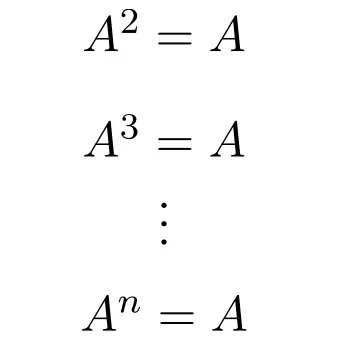
Na verdade, é por isso que esse tipo de placa recebeu esse nome. Porque em matemática a idempotência é uma operação que significa que obtemos sempre o mesmo resultado independentemente do número de vezes que é realizado.
Exemplos de matrizes idempotentes
Uma vez conhecido o conceito de matriz idempotente, veremos alguns exemplos de diferentes dimensões para finalizar seu entendimento.
Exemplo de matriz idempotente 2×2
A seguinte matriz quadrada de dimensão 2×2 é idempotente:
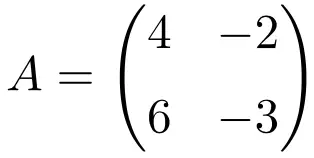
Para verificar que se trata de uma matriz idempotente, calculamos seu quadrado:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d83fda6875c8447818921c12f3196a7b_l3.png)
O resultado é idêntico, portanto mostramos que se trata de uma matriz idempotente.
Exemplo de matriz idempotente 3×3
A seguinte matriz quadrada de tamanho 3×3 é idempotente:
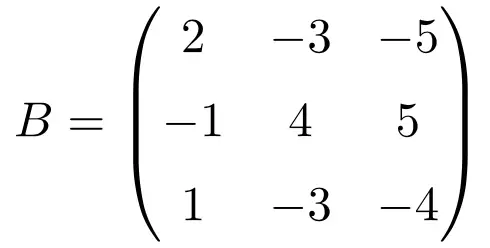
Para verificar se uma matriz idempotente corresponde, elevamos a matriz para 2:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49a3f48608f3126039c949cde6346acf_l3.png)
O resultado é igual ao da matriz original, portanto a idempotência da matriz está comprovada.
Estrutura de uma matriz idempotente 2×2
Aqui mostramos a fórmula para obter uma matriz idempotente. Caso você esteja mais interessado, você pode ver a demonstração da fórmula abaixo nos comentários, mas é um pouco tediosa então deixamos aqui diretamente com a fórmula para matrizes idempotentes :

De tal forma que os elementos da diagonal secundária de uma matriz idempotente podem ser arbitrários desde que a condição seja satisfeita
![]()
e os números na diagonal principal devem ser
![]()
E
![]()
Além de todas as matrizes descritas por esta fórmula, devemos adicionar a matriz Identidade, que também é uma matriz idempotente embora não respeite a fórmula. Se você não sabe o que é o array, pode perguntar o que é o array Identity .
Propriedades de matrizes idempotentes
Matrizes idempotentes possuem as seguintes características:
- O determinante de uma matriz idempotente é sempre 0 ou 1.
- Exceto a matriz identidade, todas as outras matrizes idempotentes são matrizes singulares ou degeneradas, ou seja, não são invertíveis.
- Qualquer matriz idempotente é diagonalizável e seus autovalores (ou autovalores) são sempre 0 ou 1.
- O traço de uma matriz idempotente é igual ao posto da matriz.
- Finalmente, existe uma relação entre matrizes idempotentes e matrizes involucionais: a matriz

é idempotente se e somente se a matriz
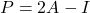
é involucional.