Neste artigo explicamos como derivar uma subtração de funções (fórmula). Você também encontrará exemplos de derivadas de subtração e exercícios resolvidos passo a passo para praticar.
Fórmula para a derivada de uma subtração
A derivada da subtração de duas funções é igual a subtrair a derivada de cada função separadamente.
![]()
Por outras palavras, diferenciar duas funções separadamente e depois subtraí-las equivale a primeiro subtrair as funções e depois calcular a derivada.
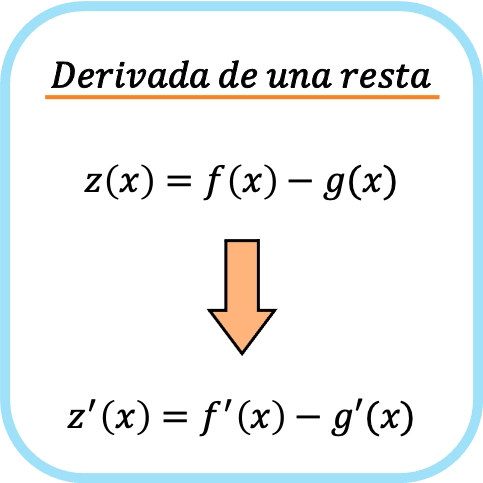
Da mesma forma, a mesma regra de diferenciação se aplica a subtrações de duas ou mais funções, portanto, se tivermos uma subtração de três, quatro, cinco,… funções, precisamos derivar cada uma separadamente e depois subtraí-las.
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc282473a7f7560eebc97db66bb8f54_l3.png)
Como você pode ver, a fórmula da derivada da diferença de funções é muito semelhante à regra da derivada da soma.
➤ Veja: derivada de uma soma de funções
Exemplos de derivada de subtração
Depois de vermos qual é a fórmula da derivada de uma subtração, passamos agora à análise de vários exemplos de derivadas deste tipo de operações para compreender completamente como são derivadas as subtrações de funções.
Exemplo 1: Derivada de uma subtração de funções potenciais
![]()
A derivada da subtração de duas funções é equivalente à diferença das derivadas de cada função separadamente. Portanto, primeiro calcularemos a derivada de cada função separadamente:
![]()
![]()
A derivada de toda a função é, portanto, a seguinte:
![]()
Exemplo 2: Derivada de uma subtração de diferentes funções
![]()
Para diferenciar funções de subtração, primeiro você deve diferenciar as duas funções separadamente e depois subtraí-las.
![]()
![]()
E depois de fazer as duas derivadas, subtraímo-las com a mesma ordem inicial:
![]()
Exemplo 3: Derivada de uma subtração quadrada
![]()
Neste caso temos uma função composta, pois é uma subtração entre três funções ao quadrado. Devemos, portanto, usar a fórmula da derivada de uma função potencial e a regra da cadeia para calcular a derivada de toda a função:
![]()
➤ Veja: fórmula para a derivada de uma potência
Exercícios resolvidos sobre a derivada de uma subtração
Derive as seguintes subtrações de funções:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Prova da derivada de uma subtração
A seguir, demonstraremos a fórmula da derivada de uma subtração de funções da definição da derivada, que é:
![]()
Então, se z é a diferença de duas funções diferentes:
![]()
![]()
Substituímos z pela subtração das funções na expressão limite:
![]()
![]()
Faremos agora uma transformação para separar a fração e obter a subtração de duas frações:
![]()
![]()
Ao aplicar as leis dos limites, podemos separar a expressão acima em dois limites diferentes. Porque o limite de uma subtração é igual à subtração dos limites:
![]()
Se você olhar de perto, cada limite corresponde à derivada de uma função, o que significa que a fórmula para a derivada de uma diferença é satisfeita:
![]()