Aqui explicamos tudo o que você precisa saber sobre monômios: o que são, quais são suas partes (e como identificá-las), os diferentes tipos de monômios, como calcular operações com monômios, o valor numérico de um monômio. .. Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo de monômios.
O que são monômios?
Em matemática, a definição de um monômio é a seguinte:
Um monômio é uma expressão algébrica formada por uma combinação de números e letras. Mais precisamente, um monômio é composto pelo produto entre um número e uma ou mais variáveis (letras) elevadas a expoentes.
Por exemplo, o termo 7x 3 y 2 é chamado de monômio porque possui um número (7) e letras diferentes (x, y).
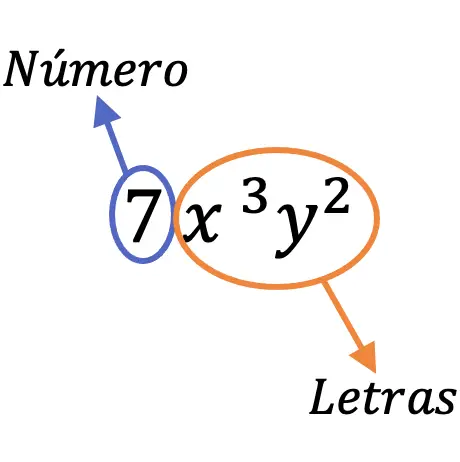
Partes de um monômio
Agora que vimos o significado de um monômio, vamos ver quais são todas as partes de um monômio:
- Coeficiente : é o número que multiplica as variáveis (ou letras) do monômio.
- Variável : é cada uma das letras que aparecem no monômio.
- Parte literal : corresponde a todas as variáveis que compõem o monômio com todos os seus respectivos expoentes.
- Grau : consiste na soma de todos os expoentes das letras que formam o monômio.
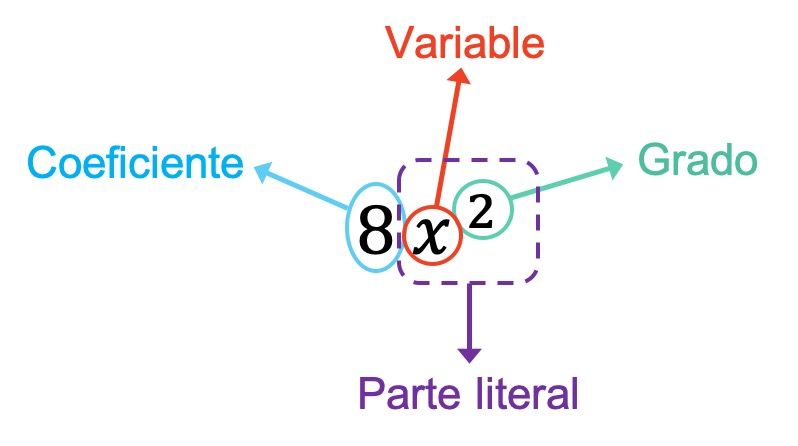
O coeficiente do monômio no exemplo acima é 8, pois é o número que multiplica as variáveis. Além disso, neste caso, o monômio possui apenas uma variável, que é x. Assim, a parte literal do monômio é formada por esta variável mais seu expoente, que é x 2 . Finalmente, o grau do monômio é 2 porque é o único expoente que possui.
Agora tente resolver o seguinte exercício sobre as partes de um monômio:
- Identifique todas as partes do seguinte monômio:
![]()
Os componentes do monômio da afirmação são:
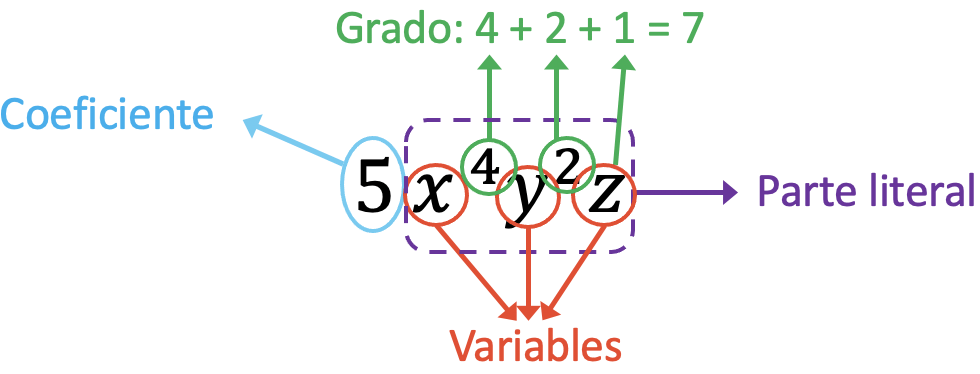
O coeficiente do monômio no problema é 5, pois é o termo que multiplica as letras. Por outro lado, as variáveis deste monômio são x, y, z. Terceiro, a parte literal do monômio corresponde à expressão x 4 y 2 z. E por fim, o grau do monômio é igual à soma de todos os expoentes das variáveis, ou seja, 7 (4+2+1=7).
Observe que quando uma letra não tem expoente, na verdade significa que ela tem 1 como expoente. Portanto, para calcular o grau do monômio do problema, adicionamos uma unidade que representa o expoente da variável z.
Tipos de monômios
Existem diferentes tipos de monômios, cada um com suas próprias propriedades. Os monômios mais importantes são monômios semelhantes, monômios homogêneos, monômios heterogêneos e monômios opostos. A seguir veremos as características de cada tipo.
monômios semelhantes
Monômios semelhantes são monômios que possuem a mesma parte literal. Portanto, dois ou mais monômios são semelhantes quando possuem as mesmas letras e expoentes.
Por exemplo, os dois monômios a seguir são semelhantes porque, embora tenham coeficientes diferentes, são formados pelas mesmas variáveis e elevados aos mesmos expoentes.
![]()
Como veremos mais adiante, este tipo de monômios é usado para resolver operações sobre monômios.
monômios homogêneos
Dois monômios são homogêneos quando seu grau absoluto é igual.
Por exemplo, os dois monômios a seguir são homogêneos porque o grau de ambos é igual a 5:
![]()
O primeiro monômio tem uma única variável elevada à potência de 5, então seu grau é 5. E o segundo polinômio tem uma variável ao quadrado e outra ao cubo, então seu grau também é 5 (2+ 3 =5).
Como você pode ver, para que dois monômios sejam homogêneos, eles não precisam ter a mesma parte literal, mas apenas o mesmo grau absoluto.
monômios heterogêneos
Monômios heterogêneos são monômios que não possuem o mesmo grau absoluto. Em outras palavras, monômios heterogêneos são o oposto de monômios homogêneos.
Os três monômios a seguir são heterogêneos porque cada um tem um grau diferente:
![]()
O primeiro monômio é de grau 8, o segundo monômio é de grau 2 e o terceiro monômio é de grau 11. Portanto, os três monômios são heterogêneos entre si.
Monômios opostos
Monômios opostos são monômios homogêneos (possuem a mesma parte literal) e, além disso, seus coeficientes são opostos, ou seja, seus coeficientes têm o mesmo valor, mas sinal oposto.
Por exemplo, os dois monômios a seguir são opostos:
![]()
Os dois monômios anteriores são opostos porque diferem apenas no sinal, o primeiro tem sinal positivo e o segundo sinal negativo.
Agora que você viu vários exemplos de monômios, talvez esteja interessado em outra expressão algébrica semelhante: o binômio . Na verdade, um binômio é composto pela adição (ou subtração) de vários monômios, por isso é interessante ver a relação entre esses dois conceitos. Você pode ver qual é o significado de binômio clicando neste link.
Operações com monômios
Para aprofundar o conceito de monômios, veremos quais operações podem ser feitas com monômios. Em particular, os monômios podem ser adicionados, subtraídos, multiplicados, divididos e aumentados. E cada tipo de operação tem suas peculiaridades, por isso iremos analisá-las uma a uma separadamente a seguir.
soma de monômios
Dois ou mais monômios só podem ser adicionados se forem monômios semelhantes. Então, a soma de dois monômios semelhantes é igual a outro monômio composto pela mesma parte literal e pela soma dos coeficientes desses dois monômios.

Exemplos de somas de monômios
Se você quiser praticar exercícios de adição de monômios, pode procurá-los no mecanismo de busca no canto superior direito, pois temos uma página inteira cheia de exercícios de adição de monômios resolvidos.
subtração de monômios
Dois ou mais monômios só podem ser subtraídos se forem monômios semelhantes. Assim, a subtração de dois monômios semelhantes é igual a outro monômio composto pela mesma parte literal e a subtração dos coeficientes desses dois monômios.

Exemplos de subtração de monômios
Você pode praticar com os exercícios passo a passo de subtração de monômios resolvidos que podem ser encontrados em nosso site. Você pode encontrá-los através do mecanismo de busca no canto superior direito.
multiplicação de monômios
O resultado da multiplicação de dois monômios é outro monômio cujo coeficiente é o produto dos coeficientes dos monômios e cuja parte literal é obtida multiplicando as variáveis que têm a mesma base, ou seja, somando seus expositores.

Assim, para resolver o produto entre dois monômios diferentes, os coeficientes devem ser multiplicados e somados os expoentes das potências que possuem a mesma base.
Por outro lado, se multiplicarmos dois monômios com potências de base diferentes, simplesmente temos que multiplicar seus coeficientes e deixar as potências iguais:
![]()
Exemplos de multiplicação de monômios
Para praticar passo a passo os exercícios resolvidos de multiplicação de monômios, você pode consultar o artigo que temos neste site. Você o encontrará facilmente com o mecanismo de busca no canto superior direito.
divisão de monômios
O resultado da divisão dos monômios é outro monômio cujo coeficiente equivale ao quociente dos coeficientes dos monômios e cuja parte literal é obtida dividindo as variáveis que possuem a mesma base, ou seja, subtraindo seus expositores.

Portanto, para dividir dois monômios diferentes, simplesmente dividimos os coeficientes entre eles e subtraímos os expoentes das potências que têm a mesma base.
Exemplos de divisão de monômios
A divisão de monômios é mais difícil do que parece, por isso recomendamos que você tente fazer passo a passo os exercícios resolvidos que temos sobre a divisão de monômios . A maneira mais rápida de encontrá-los é através do nosso mecanismo de busca no canto superior direito.
potência de um monômio
Para calcular a potência de um monômio, cada elemento do monômio deve ser elevado ao expoente da potência . Ou seja, a potência de um monômio consiste em elevar seu coeficiente e suas variáveis (letras) ao expoente da potência.

Lembre-se das propriedades das potências que quando elevamos um termo que já está elevado, os dois expoentes são multiplicados entre si. Por isso , na potência de um monômio, o expoente de cada letra é sempre multiplicado pelo expoente que indica a potência .
Exemplos de potências de monômios
É muito fácil cometer erros neste tipo de operação com monômios. É por isso que recomendamos que você pratique os exercícios que resolvemos passo a passo em nosso site. Você os encontrará rapidamente pesquisando-os no mecanismo de busca no canto superior direito.
Valor numérico de um monômio
O valor numérico de um monômio é o resultado obtido pela substituição de determinados valores pelas variáveis de um monômio.
Por exemplo, se tivermos o seguinte monômio:
![]()
Se quisermos encontrar o valor numérico do monômio anterior para
![]()
você precisa substituir a letra
![]()
do monômio por 2 e resolva as operações resultantes:
![]()
Então o valor numérico do monômio
![]()
Para
![]()
é igual a 20.
Você também pode determinar o valor numérico de uma multivariável monomial. Por exemplo, se tivermos a seguinte bivariável, ou em outras palavras, bivariável, monômio:
![]()
Para calcular o valor numérico do monômio acima quando
![]()
vale 1e
![]()
é -2, substituímos as letras pelos seus respectivos valores:
![]()
Portanto, o valor numérico do monômio do problema para
![]()
E
![]()
retorna -6.
Monômios e polinômios
Por fim, saiba que polinômios podem ser formados a partir de monômios:
Um polinômio é o agrupamento de dois ou mais monômios.
![]()
Por exemplo, o polinômio anterior resulta da adição (ou subtração) de 3 monômios heterogêneos.
Por curiosidade, quando um polinômio possui apenas 2 monômios, ele é chamado de binômio . E quando um polinômio tem exatamente 3 monômios, ele é chamado de trinômio .
Se quiser saber mais sobre polinômios, pode visitar a página principal da web, onde explicamos tudo o que você precisa saber sobre polinômios.