Aqui explicamos o que é a fórmula de identidade notável do quadrado de uma diferença (ou subtração), ou seja, mostramos como se resolve a expressão (ab) 2 . Além disso, você poderá ver exemplos e praticar com exercícios resolvidos no quadrado da diferença. E por fim, mostramos a demonstração da fórmula e a interpretação geométrica deste notável tipo de produto.
Qual é o quadrado de uma diferença (ou subtração)?
O quadrado de uma diferença , ou quadrado de uma subtração , é uma das identidades notáveis (ou produtos notáveis), ou seja, consiste em uma regra matemática que facilita o cálculo da quadratura de um binômio com dois termos: um positivo e o outro negativo.
Portanto, a expressão algébrica para o quadrado de uma diferença é (ab) 2 .
Fórmula para o quadrado de uma diferença (ou subtração)
Depois de vermos a definição deste tipo de identidade notável, veremos como resolver o quadrado de uma diferença com sua fórmula:

Assim, o quadrado de uma diferença é igual ao quadrado do primeiro termo, menos o dobro do produto do primeiro pelo segundo, mais o quadrado do segundo.
Portanto, para calcular uma diferença ou uma subtração quadrada, você não deve apenas elevar cada termo a dois, mas também multiplicá-los entre si e por 2.
É importante lembrar disso, pois um erro muito comum na subtração de quadrados é não colocar o produto entre os dois termos e apenas resolver o quadrado da diminuição e a subtração da subtração:

Não se esqueça do produto entre a e b!
Exemplos de quadrados de diferença (ou subtração)
Agora que conhecemos a fórmula do quadrado da diferença, podemos fazer cálculos com ela. E para que você possa ver como isso é feito, preparamos vários exemplos resolvidos do quadrado de uma diferença (ou subtração).
Exemplo 1
- Resolva a seguinte diferença ao quadrado:
![]()
É uma subtração ao quadrado, então você deve aplicar sua fórmula:
![]()
Então, devemos identificar quais são os valores das incógnitas
![]()
E
![]()
da fórmula. Nesse caso,
![]()
é a variável
![]()
E
![]()
corresponde ao número 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
Observe que o sinal negativo não faz parte de
![]()
mas você deve sempre pegar o número sem o sinal para aplicar corretamente a fórmula.
Portanto, já conhecemos os valores de
![]()
e de
![]()
Portanto, precisamos apenas substituir esses valores na fórmula:

Exemplo 2
- Calcule o seguinte binômio de uma subtração quadrada:
![]()
A fórmula para a diferença quadrada é:
![]()
Então, primeiro precisamos identificar os valores de
![]()
e de
![]()
da fórmula. Neste problema,
![]()
representa o monômio
![]()
E
![]()
é equivalente ao termo independente do binômio, ou seja, 2:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868a41eb665f5bc94959448547c060d5_l3.png)
Finalmente, uma vez que sabemos o valor dos parâmetros
![]()
E
![]()
, simplesmente aplicamos a fórmula binomial para subtração ao quadrado:
![Rendered by QuickLaTeX.com \begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5e88231a654b23a306e53e17d175d25_l3.png)
Prova da fórmula do quadrado de uma diferença
Deduziremos então de onde vem a fórmula do quadrado de uma subtração. Embora você não precise memorizar a prova, ainda é bom entender a matemática por trás dela.
Se partirmos da expressão do binômio de todas as subtrações:
![]()
Obviamente, a potência anterior é igual ao produto do fator
![]()
multiplicado por si mesmo:
![]()
Agora multiplicamos os dois parênteses aplicando a propriedade distributiva:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
E só temos que agrupar termos semelhantes para terminar de provar a fórmula:
![]()
Para que a fórmula do quadrado de uma subtração seja provada matematicamente:
![]()
A título de curiosidade, a expansão da expressão binomial de uma subtração quadrada também é conhecida como trinômio quadrado perfeito.
Interpretação geométrica do quadrado de uma diferença
Para finalizar a compreensão da noção de quadrado de uma diferença, veremos como interpretar geometricamente esta notável igualdade.
Observe o seguinte quadrado com lados de comprimento
![]()
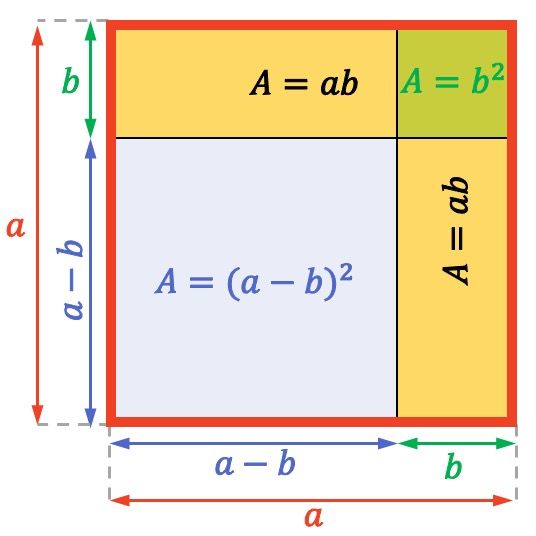
A área (ou área de superfície) de um quadrado ou retângulo é calculada multiplicando dois de seus lados adjacentes. Portanto, a área de todo o quadrado inteiro acima é
![]()
Da mesma forma, a área de cada retângulo amarelo é igual a
![]()
E finalmente, o pequeno quadrado mostrado no canto superior direito tem uma área de
![]()
Isto significa que um quadrado de lado
![]()
cuja superfície é
![]()
pode ser decomposto na área de um quadrado de dimensão
![]()
menos 2 vezes a área de um retângulo de dimensões
![]()
E
![]()
, mais a área de um quadrado lateral
![]()
Resumindo, a fórmula do quadrado de uma diferença também pode ser verificada geometricamente:
![]()
Problemas resolvidos do quadrado de uma diferença (ou subtração)
Para que você possa praticar, deixamos vários exercícios resolvidos passo a passo sobre o produto notável do quadrado de uma diferença. Lembre-se de que você pode nos escrever qualquer dúvida abaixo nos comentários.
Exercício 1
Resolva as seguintes subtrações ao quadrado:
![]()
![]()
![]()
![]()
![]()
Para encontrar todas as identidades notáveis do problema, basta aplicar a fórmula do quadrado de uma diferença, que é:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-138b359ce2e8f8b1012c6ecf1b7fb9b0_l3.png)
Exercício 2
Determine os seguintes quadrados das diferenças de duas quantidades aplicando a fórmula:
![]()
![]()
![]()
Para determinar todos os produtos notáveis do problema é necessário usar a fórmula de subtração ao quadrado:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c73b9ba584f955a0cae5564a2226d465_l3.png)
Para resolver a seção B), você precisa lembrar que se uma raiz for quadrada, ela será simplificada:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38cd9e9855f7f79f607247ccc731e297_l3.png)
Os monômios da última subtração ao quadrado possuem coeficientes fracionários, então para resolvê-lo precisamos usar as propriedades das frações:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46106420913cc7a370e2f5215af0f2a2_l3.png)