Nesta página você encontrará a fórmula do quadrado de uma soma, ou seja, a identidade notável (a+b) 2 . Você também poderá ver exemplos e exercícios resolvidos de somas quadradas. E, além disso, você descobrirá as propriedades geométricas escondidas neste notável produto.
Qual é o quadrado de uma soma?
O quadrado de uma soma é uma das identidades notáveis (ou produtos notáveis), portanto é uma regra matemática que permite calcular rapidamente a potência de um binômio com dois termos positivos quadrados.
Assim, o quadrado de uma soma consiste em dois termos diferentes somados e elevados ao quadrado, ou seja, a expressão algébrica para o quadrado de uma soma é (a+b) 2 .
Fórmula para o quadrado de uma soma
Dada a definição matemática deste notável tipo de identidade, veremos agora qual é a fórmula do quadrado de uma soma :

De modo que o quadrado de uma soma é igual ao quadrado do primeiro termo, mais o dobro do produto do primeiro pelo segundo, mais o quadrado do segundo.
Assim, para resolver uma soma quadrada, não basta elevar cada adição a dois, mas, além disso, as duas adições devem ser multiplicadas entre si e por 2.
É importante lembrar disso, pois um erro muito comum na hora de somar os quadrados é esquecer o produto entre os dois termos e calcular apenas os quadrados:

Lembre-se de não deixar nenhum termo fora da fórmula!
Por outro lado, lembre-se que a fórmula de uma subtração ao quadrado (ou ao quadrado de uma subtração) é muito semelhante à que acabamos de ver, mas tem uma diferença que muda completamente o resultado. Se você não tem certeza de como é isso, você pode verificar aqui o que é a fórmula de subtração ao quadrado e como ela é aplicada.
Exemplos de soma quadrada
Aqui estão vários exemplos práticos para que você possa ver como elevar ao quadrado uma soma:
Exemplo 1
- Calcule a seguinte soma ao quadrado aplicando a fórmula:
![]()
A fórmula para uma soma quadrada é:
![]()
Devemos primeiro identificar os parâmetros
![]()
E
![]()
da fórmula. Nesse caso,
![]()
representa o
![]()
do par e
![]()
corresponde ao número 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Bem, como agora sabemos os valores de
![]()
e de
![]()
Podemos aplicar a fórmula para encontrar o resultado do quadrado da soma:

Exemplo 2
- Resolva a seguinte expressão para o quadrado de uma soma:
![]()
A fórmula para o quadrado de uma soma é:
![]()
Então neste problema
![]()
é o monômio
![]()
E por outro lado,
![]()
é o termo independente 4:
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
Finalmente, uma vez identificados os valores de
![]()
e de
![]()
, aplicamos a fórmula da soma quadrada para resolver o produto notável:
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
Prova da fórmula do quadrado de uma soma
A seguir deduziremos a fórmula que acabamos de ver do quadrado de uma soma, para que você entenda de onde ela vem.
Partindo de um binômio positivo elevado a 2:
![]()
A potência acima é obviamente equivalente ao fator
![]()
multiplicado por si mesmo:
![]()
Então, multiplicamos os dois parênteses usando a propriedade distributiva:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Por fim, a partir dos termos resultantes, agrupamos aqueles que são semelhantes:
![]()
E já chegamos na expressão polinomial da fórmula, então está provado:
![]()
Embora possa ser difícil de acreditar, a fórmula do quadrado de uma soma também funciona para fatorar polinômios quadráticos . Caso você não saiba o que é, a fatoração polinomial é um procedimento frequentemente usado em matemática para simplificar a expressão de um polinômio. Descubra como isso é feito clicando no link acima.
Interpretação geométrica do quadrado de uma soma
Até agora vimos como o quadrado de uma soma é calculado matematicamente, mas este produto notável também pode ser interpretado geometricamente.
Observe o seguinte quadrado cujos lados medem
![]()
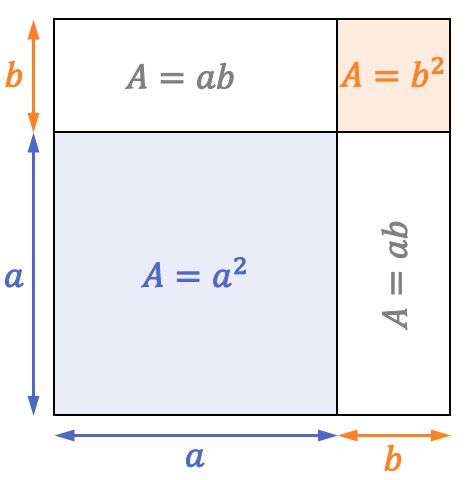
A área de um quadrado é igual ao comprimento de um de seus lados ao quadrado. Portanto, como o lado do quadrado anterior é
![]()
sua área (ou superfície) é igual a
![]()
Bem, como você pode ver na representação quadrada, um quadrado com área de
![]()
retângulos com duas áreas
![]()
e outro quadrado de superfície
![]()
Portanto, a fórmula da soma de um quadrado também se cumpre do ponto de vista geométrico:
![]()
Problemas resolvidos do quadrado de uma soma
A seguir deixamos vocês com vários exercícios de soma de quadrados resolvidos passo a passo para que você possa praticar e assim terminar de entender o conceito. Você pode nos escrever todas as suas perguntas nos comentários e teremos o maior prazer em respondê-las. 💭💭💭
Exercício 1
Determine as seguintes somas ao quadrado:
![]()
![]()
![]()
![]()
Para resolver todas as identidades notáveis do problema basta aplicar a fórmula do quadrado de uma soma:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Exercício 2
Resolva a seguinte soma quadrada de dois termos aplicando a fórmula:
![]()
![]()
![]()
Para calcular todos os produtos notáveis do problema você deve usar a fórmula da soma quadrada:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
Na seção B) você precisa lembrar que se uma raiz for quadrada, ela será simplificada:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
Os monômios da última soma ao quadrado possuem coeficientes fracionários, então para resolvê-lo também precisamos usar as propriedades das frações:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Exercício 3
Encontre a seguinte potência aplicando a fórmula do quadrado de uma soma e sem usar a calculadora:
![]()
Em primeiro lugar, o número dezassete pode ser dividido na soma de 10 mais 7:
![]()
Então convertemos a potência para uma soma quadrada. Portanto, podemos agora aplicar a fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
Resumindo, o resultado da potencialização é:
![]()
Como você viu neste exercício, a fórmula da soma quadrada também é útil para calcular potências de números grandes sem usar uma calculadora.
Quadrado de uma soma de 3 termos
Às vezes podemos descobrir que precisamos resolver o quadrado de três termos adicionados, ou seja, (a+b+c) 2 . Logicamente, nestes casos não podemos utilizar a fórmula que explicamos, pois dentro dos parênteses temos um trinômio em vez de um binômio. Portanto, é necessário usar uma fórmula diferente.
A fórmula do quadrado da soma de 3 termos é a seguinte:
![]()
Vamos ver como esta fórmula é aplicada através de um exemplo:
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
Como você pode ver, adicionar um elemento à fórmula torna o resultado muito mais complicado.