Nesta página você pode aprender o que é uma matriz Hermitiana, também conhecida como matriz Hermitiana. Você encontrará exemplos de matrizes hermitianas, todas as suas propriedades e a forma que esses tipos de matrizes possuem para entendê-las perfeitamente. Finalmente, também explicamos como decompor qualquer matriz complexa na soma de uma matriz Hermitiana mais uma matriz anti-Hermitiana.
O que é uma matriz Hermitiana ou Hermitiana?
Uma matriz Hermitiana , ou também chamada de matriz Hermitiana, é uma matriz quadrada com números complexos que tem a característica de ser igual à sua transposta conjugada .
![]()
Ouro
![]()
é a matriz transposta conjugada de
![]()
.
A título de curiosidade, este tipo de matriz tem esse nome em homenagem a Charles Hermite, um matemático francês do século XIX que fez importantes pesquisas em matemática, particularmente na área de álgebra linear.
A razão para nomear esta matriz desta forma foi que ela mostrou que os autovalores (ou autovalores) dessas matrizes particulares são sempre números reais, mas explicaremos isso com mais detalhes em Propriedades das Matrizes Hermitianas.
Finalmente, esta matriz às vezes também pode ser chamada de matriz autoadjunta, embora isso seja muito raro.
Exemplos de matrizes Hermitianas
Depois de vermos a definição da matriz Hermitiana (ou matriz Hermitiana), vejamos alguns exemplos de matrizes Hermitianas de diferentes dimensões:
Exemplo de matriz Hermitiana de ordem 2×2
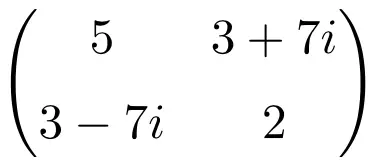
Exemplo de uma matriz Hermitiana de dimensão 3 × 3
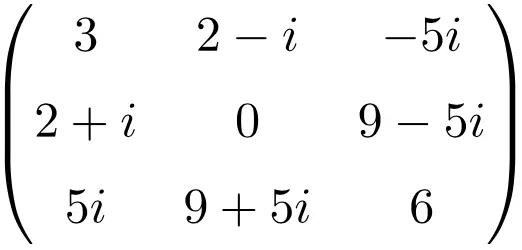
Exemplo de uma matriz Hermitiana de tamanho 4×4
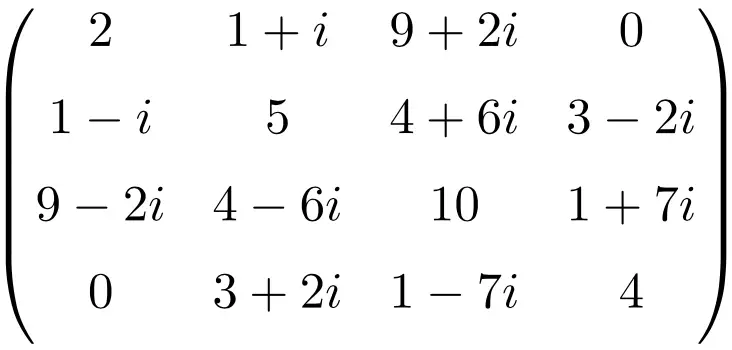
Todas essas matrizes são hermitianas porque a matriz transposta conjugada de cada uma é igual à própria matriz.
Estrutura de uma matriz Hermitiana
As matrizes hermitianas possuem uma estrutura muito fácil de lembrar: são formadas por números reais na diagonal principal, e o elemento complexo localizado na i-ésima linha e na j-ésima coluna deve ser o conjugado do elemento encontrado na j-ésima linha e a i-ésima coluna.
Aqui estão alguns exemplos de estruturas de matriz Hermitiana.
Estrutura hermitiana 2×2
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7c3eb7e683eabc86f70d307886a25f6_l3.png)
Estrutura Hermitiana 3×3
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f7d10b69e2e0edf09a8dd5eca195c00_l3.png)
Estrutura hermitiana 4×4
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d2a67c9e5748a431c83128df2b720df_l3.png)
Propriedades da matriz Hermitiana
Veremos agora quais são as propriedades deste tipo de matriz quadrada complexa:
- Qualquer matriz hermitiana é uma matriz normal . Embora nem todas as matrizes normais sejam matrizes Hermitianas.
- Qualquer matriz hermitiana é diagonalizável. Além disso, a matriz diagonal resultante contém apenas elementos reais.
- Portanto, os autovalores (ou autovalores) de uma matriz Hermitiana são sempre números reais. Esta propriedade foi descoberta por Charles Hermite, e por esta razão ele teve a honra de chamar esta matriz tão especial de Hermitiana.
- Da mesma forma, os autoespaços de uma matriz Hermitiana são ortogonais dois por dois: existe uma base ortonormal de

consistindo em vetores próprios (vetores próprios) da matriz.
- Uma matriz de números reais, ou seja, que nenhum elemento tem parte imaginária, é hermitiana se e somente se for uma matriz simétrica. Como por exemplo a matriz identidade 2×2 .
- Uma matriz Hermitiana pode ser expressa como a soma de uma matriz simétrica real e uma matriz antissimétrica imaginária.
![]()
- A soma (ou subtração) de duas matrizes Hermitianas é igual a outra matriz Hermitiana, porque:
![]()
- O resultado do produto de uma matriz Hermitiana por um escalar é outra matriz Hermitiana se o escalar for um número real.
![]()
- O produto de duas matrizes Hermitianas geralmente não é mais Hermitiano. Porém, o produto é hermitiano quando as duas matrizes são comutáveis, ou seja, quando o resultado da multiplicação das duas matrizes é o mesmo independente da direção em que são multiplicadas, pois então a seguinte condição das operações com transposta conjugada matrizes:
![]()
- Se uma matriz Hermitiana for invertível, sua inversa também será uma matriz Hermitiana.
![]()
- O determinante de uma matriz Hermitiana é sempre equivalente a um número real. Aqui está a prova desta propriedade:
![]()
Sedento
![]()
:
![]()
Portanto, para que esta condição seja atendida, o determinante de uma matriz Hermitiana deve necessariamente ser um número real. Desta forma, o conjugado do resultado é igual ao próprio resultado.
Decomposição de uma matriz complexa em uma matriz Hermitiana e uma matriz anti-Hermitiana
Qualquer matriz com elementos complexos pode ser decomposta na soma de uma matriz Hermitiana mais outra matriz anti-Hermitiana . Mas para isso você precisa conhecer as seguintes particularidades desses tipos de matrizes:
- A soma de uma matriz quadrada complexa mais seu conjugado transposto dá uma matriz Hermitiana.
![]()
- A diferença entre uma matriz quadrada complexa e seu conjugado transposto dá uma matriz anti-Hermitiana (ou anti-Hermitiana).
![]()
- Portanto, todas as matrizes complexas podem ser decompostas na soma de uma matriz Hermitiana e uma matriz anti-Hermitiana. Este teorema é conhecido como decomposição de Teoplitz :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74e1d9a0d55d77dd927109e42986c200_l3.png)
Onde C é a matriz complexa que queremos decompor, C* seu conjugado transposto e finalmente A e B são respectivamente as matrizes Hermitiana e anti-Hermitiana nas quais a matriz C é decomposta.