Matriz unitária

Nesta página explicamos o que é a matriz unitária e, além disso, ilustramos com diversos exercícios para que seja bem compreendida. Você também descobrirá quais são todas as propriedades desse tipo de matriz tão importantes para a álgebra linear.

O que é uma matriz unitária?

A definição de matriz unitária é a seguinte:

Uma matriz unitária é uma matriz complexa que multiplicada por sua matriz transposta conjugada é igual à matriz identidade. Ou seja, a seguinte condição é atendida:

U\cdot U^* = U^* \cdot U =I

Ouro

U

é uma matriz unitária e

U^*

sua transposta conjugada.

Portanto, esta condição implica que a inversa de uma matriz unitária é a sua transposta conjugada , pois, segundo a definição de uma matriz inversa, uma matriz é a inversa de outra se o seu produto for equivalente à matriz d’identificar .

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Portanto, uma matriz unitária será sempre uma matriz regular ou não degenerada , pois sempre terá uma inversa.

Por outro lado, o análogo de uma matriz unitária num ambiente de números reais é a matriz ortogonal , e neste caso é verdade que a matriz unitária multiplicada pela sua transposta é igual à matriz identidade.

U\cdot U^t = U^t \cdot U =I

Portanto, neste caso a matriz inversa de U seria diretamente a sua matriz transposta (ou transposta).

Exemplos de matrizes unitárias

Exemplo de uma matriz unitária de dimensão 2×2

Depois de vermos o conceito de matriz unitária, veremos um exemplo de matriz unitária 2×2 para entendê-la bem:

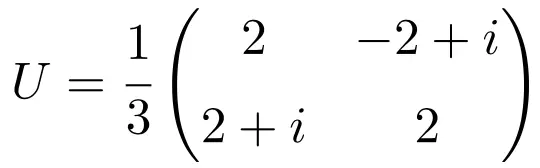
exemplo de matriz unitária de dimensão 2x2

Esta matriz é unitária porque a multiplicação dela mesma pela sua matriz conjugada dá a matriz Identidade (ou Unidade):

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

E, como vimos anteriormente, qualquer matriz unitária é comutável com sua transposta conjugada:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Exemplo de matriz diagonal unitária

A matriz diagonal composta apenas pelo número complexo i também é um exemplo de matriz unitária, independente da dimensão da matriz. Abaixo você tem um exercício resolvido que ilustra isso com uma matriz unitária de dimensão 3 × 3:

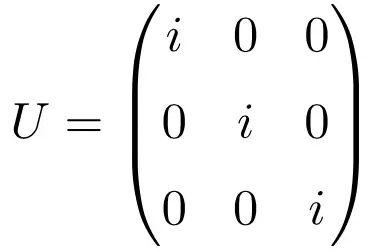
exemplo de matriz unitária de dimensão 3x3

Observe que se resolvermos o produto da matriz por sua transposta conjugada, isso dá a matriz Identidade como solução:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

E a mesma coisa acontece se multiplicarmos as matrizes ao contrário:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

A característica desta matriz é que ela serve como exemplo de matriz unitária de qualquer dimensão, pois cada vez que a matriz é formada pelo número imaginário i na diagonal principal e os demais elementos são zero (0 ) será uma matriz unitária.

Propriedades de uma matriz unitária

As propriedades das matrizes unitárias são as seguintes:

  • Obviamente, qualquer matriz unitária é uma matriz normal . Embora nem todas as matrizes normais sejam matrizes unitárias.
  • Todas as matrizes unitárias são diagonalizáveis, ou seja, podem ser transformadas em matrizes diagonais.
  • O valor absoluto do determinante de uma matriz unitária é sempre igual a 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • para todos

    n

    , o conjunto de todas as matrizes unitárias

    n\times n

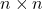
    com a operação de produto matricial, eles formam um grupo, denominado grupo de unidades.

  • Portanto, a multiplicação de duas matrizes unitárias da mesma ordem dá outra matriz unitária.
  • O módulo de todos os autovalores (ou autovalores) de uma matriz unitária é sempre igual a 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • Os autoespaços deste tipo de matriz são ortogonais.

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima