Nesta página você verá o que são matrizes complexas, matrizes conjugadas e matrizes transpostas conjugadas. Agora eles se parecem muito com você, mas você verá como no final da página entenderá perfeitamente a diferença entre cada um. Além disso, veremos exemplos de cada tipo e suas propriedades.
matriz complexa
Antes de ver a explicação da matriz conjugada e da matriz conjugada transposta, vamos revisar o conceito de matriz complexa:
O que é uma matriz complexa?
Uma matriz complexa é uma matriz que possui um determinado número complexo entre seus elementos.
Lembre-se que um número complexo ou imaginário é um número composto por uma parte real e uma parte imaginária, indicada pela letra i. Por exemplo:
![]()
.
Exemplos de matrizes complexas
Vejamos alguns exemplos de matrizes multidimensionais complexas:
Exemplo de matriz complexa de ordem 2 × 2
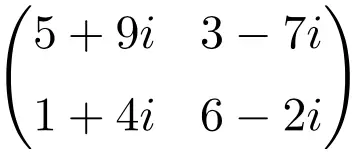
Exemplo de uma matriz complexa de dimensão 3×3
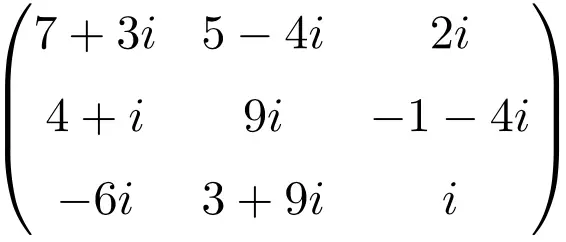
Exemplo de uma matriz complexa de tamanho 4×4
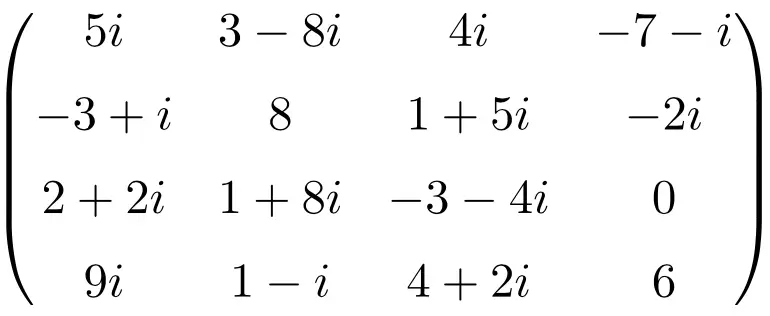
matriz conjugada
Depois de vermos qual é a definição de uma matriz complexa, vamos ver o que são uma matriz conjugada e uma matriz conjugada transposta:
O que é uma matriz conjugada?
Uma matriz conjugada é uma matriz complexa em que todos os seus elementos foram substituídos pelos seus conjugados, ou seja, o sinal da parte imaginária de todos os seus números complexos foi alterado.
A matriz conjugada de
![]()
é expresso por uma barra horizontal acima:
![]()
.
Exemplo de uma matriz conjugada
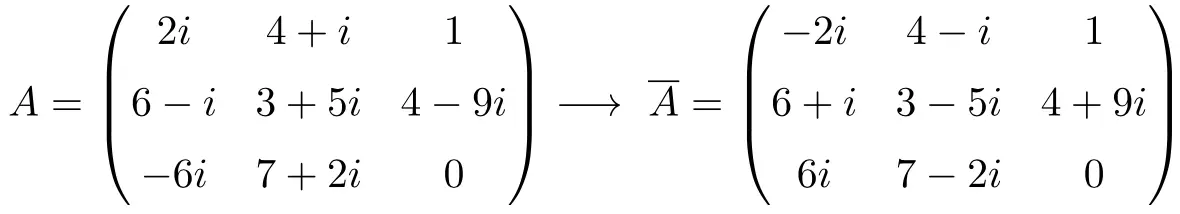
Propriedades da matriz conjugada
As características deste tipo de matriz são as seguintes:
- O conjugado de uma matriz conjugada é a matriz original.
![]()
- Adicionar (ou subtrair) duas matrizes e conjugar o resultado é o mesmo que primeiro conjugar as duas matrizes separadamente e depois adicioná-las (ou subtraí-las).
![]()
- O produto conjugado de duas matrizes é igual a conjugar as duas matrizes separadamente e depois calcular a multiplicação da matriz.
![]()
- Multiplicar uma matriz por um escalar e conjugar o resultado é o mesmo que primeiro fazer os conjugados do escalar e da matriz e depois resolver o produto.
![]()
- Transpor uma matriz e depois conjugá-la significa primeiro conjugar a matriz e depois transpô-la.
![]()
- Fazer o inverso de uma matriz e depois conjugá-la é o mesmo que conjugar a matriz e depois invertê-la.
![]()
- A classificação de uma matriz conjugada é igual à classificação da mesma matriz não conjugada.
![]()
- É indiferente calcular o traço de uma matriz conjugada ou calcular o traço da mesma matriz sem conjugação e depois conjugar o resultado.
![]()
- Por fim, tomar o determinante de uma matriz conjugada equivale a calcular o conjugado do resultado do determinante da mesma matriz sem conjugação.
![]()
Matriz transposta conjugada
Por fim, depois de ver como conjugar uma matriz, vamos passar ao conceito de matriz transposta conjugada:
O que é uma matriz transposta (ou transposta) conjugada?
A matriz conjugada transposta (ou transposta) é aquela obtida após ter transposto uma matriz e feito seu conjugado.
Este tipo de matriz também é chamada de matriz adjunta ou simplesmente matriz adjunta. Além disso, geralmente é representado por um asterisco
![]()
, embora existam matemáticos que o desenham como
![]()
qualquer
![]()
.
Exemplo de matriz de transposição conjugada
Aqui está um exemplo de cálculo da transposta (ou transposta conjugada) de uma matriz:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
Primeiro transpomos a matriz A:
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
E então calculamos a matriz conjugada da transposta, ou seja, mudamos o sinal da parte imaginária de todos os números complexos:
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
Portanto, o resumo do cálculo da matriz transposta conjugada é:
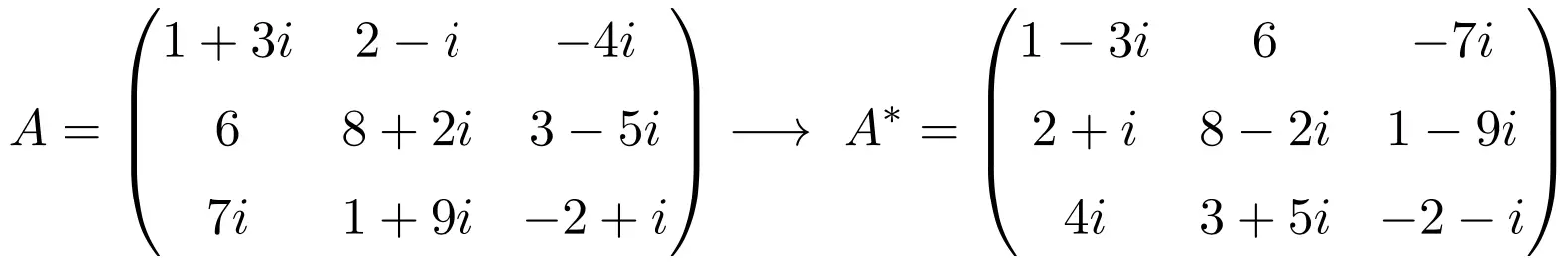
Propriedades da matriz transposta conjugada
As propriedades deste tipo de matriz quadrada são as seguintes:
- A matriz transposta conjugada de uma matriz previamente transposta e conjugada é a matriz original.
![]()
- A propriedade de adição de matrizes transpostas conjugadas afirma que adicionar (ou subtrair) duas matrizes e depois aplicar esta operação ao resultado é equivalente a primeiro fazer a transposta conjugada de cada matriz e depois adicionar (ou subtrair) os resultados.
![]()
- Multiplicar duas matrizes e depois fazer sua transposta conjugada dá o mesmo resultado que o produto inverso das matrizes transpostas conjugadas.
![]()
- Calcular a matriz transposta conjugada do produto de um escalar e uma matriz é o mesmo que conjugar o número complexo e encontrar a transposta conjugada da matriz separadamente e depois multiplicar.
![]()
- Se a matriz for invertível, a ordem em que as operações de inversão da matriz e de transposição conjugada são realizadas é irrelevante.
![]()