Nesta página você verá o que é uma matriz normal, bem como exemplos de matrizes normais. Além disso, você encontrará as propriedades deste tipo de matrizes e exercícios resolvidos passo a passo.
O que é uma matriz normal?
A definição normal da matriz é:
Uma matriz normal é uma matriz complexa que multiplicada por sua matriz transposta conjugada é igual ao produto da transposta conjugada por ela mesma.
![]()
Ouro
![]()
é a matriz transposta conjugada de
![]()
.
Porém, se forem matrizes de números reais , a condição anterior equivale a dizer que uma matriz comuta com a sua transposta, ou seja:
![]()
Porque, obviamente, a matriz transposta conjugada de uma matriz real é simplesmente a matriz transposta (ou transposta).
Exemplos de matrizes normais
Exemplo com números complexos
A seguinte matriz quadrada complexa de dimensão 2×2 é normal:
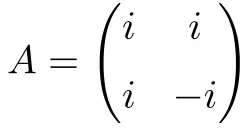
A demonstração de sua normalidade está anexada abaixo:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44b98cec879a8332c462d2393fbfbba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fddc406493ac1c81c86edf1ad6e58d0b_l3.png)
Exemplo com números reais
A seguinte matriz quadrada com números reais de ordem 2 também é normal:
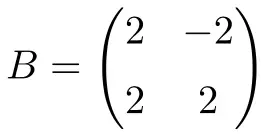
Neste caso, por só possuir números reais, para provar que é normal basta verificar que a matriz é comutável com a sua transposta:
![Rendered by QuickLaTeX.com \displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a320a8e300315c6a48bb8095266408ca_l3.png)
![Rendered by QuickLaTeX.com \displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6ad5bd62deeb5bcbf561a2ee6b29741_l3.png)
Propriedades de matrizes normais
Matrizes normais têm as seguintes características:
- Todas as matrizes normais são matrizes diagonalizáveis.
- Cada matriz unitária também é uma matriz normal.
- Da mesma forma, uma matriz Hermitiana é uma matriz normal.
- Da mesma forma, uma matriz anti-hermitiana é uma matriz normal.
- Se A é uma matriz normal, os autovalores (ou autovalores) da matriz transposta conjugada A* são os autovalores conjugados de A.
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91ee46b5f8dda0d51ecb57474f5b816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-48c80a017a9afd8b4cf3923757f4e945_l3.png)
- Nas matrizes normais, os autovetores (ou autovetores) associados aos diferentes autovalores são ortogonais.
- Se uma matriz é composta apenas por números reais e é simétrica , é ao mesmo tempo uma matriz normal.
- Da mesma forma, uma matriz real antissimétrica também é uma matriz normal.
- Finalmente, qualquer matriz ortogonal formada por números reais também é uma matriz normal.
Exercícios resolvidos para matrizes normais
Exercício 1
Verifique se a seguinte matriz complexa de dimensão 2 × 2 é normal:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff27d19373c5a4dc8e95472ec295c657_l3.png)
Para mostrar que a matriz é normal devemos primeiro calcular sua transposta conjugada:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17c96c654ce5b978f90a905b973d5ae7_l3.png)
E agora fazemos a verificação multiplicando a matriz A pela matriz A* nas duas direções possíveis:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36212e1d12cf35ea5dd27bd91d77ee56_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3db0fc8fdc948037452b4c6275896686_l3.png)
O resultado de ambas as multiplicações é o mesmo, então a matriz A é normal.
Exercício 2
Mostre que a seguinte matriz real de tamanho 2 × 2 é normal:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854e13859be417985691b5ed6d2a050f_l3.png)
Como neste caso se trata de um ambiente apenas com números reais, basta verificar que o produto matricial entre a matriz A e sua transposta dá o mesmo resultado qualquer que seja o sentido da multiplicação:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1b6314188f394b3053d3dac0613cf5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2b33f892cd29c0ee232b88eaa4946cc_l3.png)
O resultado de ambos os produtos é o mesmo, então a matriz A é normal.
Exercício 3
Determine se a seguinte matriz de números complexos de ordem 2 é normal:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00075db37b045e08349f7d5b3f679570_l3.png)
Para verificar se a matriz é normal, devemos primeiro calcular sua transposta conjugada:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0b39733376eb2aef269012eb1d6c24be_l3.png)
E agora verificamos se a matriz A e sua transposta conjugada são comutáveis:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c207cb9842dacbaf9bc59d4aaff00473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bcf52f3da81fd7c56b090604c2b6f368_l3.png)
O resultado de ambas as multiplicações é o mesmo, então a matriz A é normal.
Exercício 4
Verifique se a seguinte matriz real de dimensão 3×3 é normal:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92ee07759c3e6e88af5a68479b5833ea_l3.png)
Sendo a matriz inteiramente composta por elementos reais, basta verificar que o produto matricial entre a matriz A e sua transposta é independente do sentido da multiplicação:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc7ee02c75239b430c7fc2418f43e343_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e661b877ee225983c797584e2b61d429_l3.png)
O resultado de ambos os produtos é o mesmo, então a matriz A é normal.
Exercício 5
Determine se a seguinte matriz complexa de ordem 3×3 é normal:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81ca0ac1da07c151a62dcfb06b4be877_l3.png)
Primeiro, calculamos a transposta conjugada da matriz:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd0a2dfe1b8bfe18020ab68c1eb3bda6_l3.png)
Agora precisamos fazer as multiplicações de matrizes entre a matriz A e sua transposta conjugada em ambas as direções possíveis. No entanto, a matriz transposta conjugada de A é igual à própria matriz A, portanto é uma matriz Hermitiana. E, portanto, das propriedades das matrizes normais segue-se que A é uma matriz normal , porque toda matriz hermitiana é uma matriz normal.